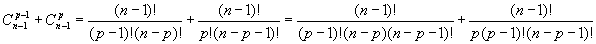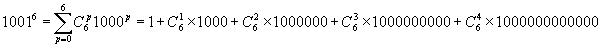Cours sur la récursivité

Le triangle de Pascal est le tableau des coefficients qui sont utilisés pour le développement de certaines expressions comme (a+b)² ou (a+b)n.

Cela s'appelle la "formule du binôme de Newton". Les coefficients s'appellent les "coefficients binomiaux" ou "coefficients du binôme".

Ce triangle est le suivant :

0 : 1          (a+b)0 = 1 
1 : 1 1        (a+b)1 = 1*a + 1*b
2 : 1 2 1      (a+b)2 = 1*a2 + 2*a*b + 1*b2
3 : 1 3 3 1    (a+b)3 = 1*a3 + 3*a²*b + 3*a*b² + 1*b3
4 : 1 4 6 4 1  (a+b)4 = 1*a4 + 4*a3*b + 6*a²*b² + 4*a*b3 + 1*b4

On obtient chaque coefficient en additionnant le nombre qui lui est situé au-dessus ainsi que celui qui lui est situé au-dessus à gauche.

Exemples :
- on obtient le 6 en faisant 3+3
- on obtient le 4 qui est après le 6 en faisant 3+1.

Le numéro qui est en tête de chaque ligne de ce triangle est la puissance à laquelle "a+b" est élevé;ainsi pour la puissance 4,"(a+b)4" admet les coefficients 1, 4, 6, 4, 1 qu'on voit dans l'expression développée.
Etudions l'algorithme nécessaire à l'affichage de ce triangle :
- on remarque que la diagonale est toujours à 1 ---> point d'appui
- on remarque que la première colonne est toujours à 1 ---> point d'appui
- pour tout autre élément qui se trouve à la ligne y et colonne x, on affiche la somme de :
-- l'élément de coordonnées y-1,x
-- l'élément de coordonnées y-1,x-1

function comb(x, y: integer): integer;
begin
  if (x = 1) or //--- point d'appui : la première colonne
    (y = x) //--- point d'appui : la diagonale
    then comb := 1
  else
    comb := comb(x, y - 1) + comb(x - 1, y - 1); //--- appel récursif
end;

On voit ici la définition récursive, car tout élément du tableau est défini par deux autres éléments qui sont inconnus, chacun étant défini par deux autres et ainsi de suite, excepté la diagonale et la première colonne; c'est grâce à ces deux indices qu'on va déterminer tout le tableau.

Voici le programme qui affiche le triangle de Pascal :

procedure tform1.button1Click(sender: tobject);
var ligne, colonne: integer;
 
  function comb(x, y: integer): integer;
  begin
    if (x = 1) or (y = x) then
      comb := 1
    else
      comb := comb(x, y - 1) + comb(x - 1, y - 1);
  end;
begin
  for ligne := 1 to 15 do
    for colonne := 1 to ligne do
      canvas.textOut(colonne * 30, ligne * 30, inttostr(comb(colonne, ligne)));
end;

Et maintenant, un peu de maths :

Formule du triangle de Pascal

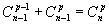
Démonstration combinatoire

Soit E un ensemble à n éléments et a un élément de E.
Notons :
A l'ensemble des parties de E à p éléments (p n),
B l'ensemble des parties à p éléments de E contenant a,
C l'ensemble des parties à p éléments de E ne contenant pas a.
Le cardinal de A est .
Comme B est l'ensemble des parties à p-1 éléments de auxquelles on a ajouté a, le cardinal de B est égal à celui de l'ensemble des parties à p-1 éléments de . D'où Card(A)=
Comme C est l'ensemble des parties à p éléments de , Card(C)= .
A étant la réunion disjointe de B et C, on a Card(A)=Card(B)+Card(C), d'où le résultat.

Démonstration directe

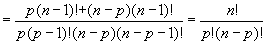
Formule du binôme de Newton

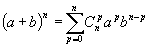
Démonstration combinatoire

Le coefficient du terme est égal au nombre de façons de choisir simultanément p paires de parenthèses contenant a parmi les n, soit , d'où le résultat (c'est aussi le nombre de façons de choisir simultanément n-p paires de parenthèses contenant b parmi les n, soit . Or ... ).

Démonstration par récurrence

La formule se vérifie aisément pour n=0.

Supposons qu'elle est vraie pour n fixé et montrons qu'alors

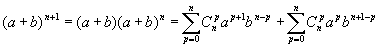
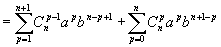
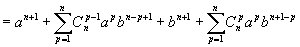
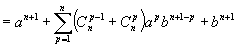
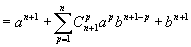
d'après la formule de Pascal, d'où le résultat.

La formule étant vraie pour n=0 et l'étant pour n+1 sous l'hypothèse qu'elle l'est pour n fixé, est donc vraie pour tout entier naturel n en vertu de l'axiome de récurrence.

Une application amusante

Calculons 1001^6.

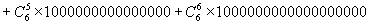
= 1+6x1000+15x1000000+20x1000000000+15x1000000000000+6x1000000000000000+1000000000000000000
Nous laissons au lecteur le soin de faire l'addition !

Un résultat remarquable

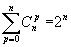
Démonstration 1

Le résultat est immédiat en faisant a=b=1 dans la formule du binôme !

Démonstration 2

La somme de tous les pour n fixé (la somme de tous les coefficients binomiaux d'une ligne du triangle de Pascal) est égale au nombre de façons de choisir simultanément entre 0 et n éléments d'un ensemble à n éléments, c'est à dire exactement au nombre de parties de cet ensemble, soit 2^n.

On montre directement que le nombre de parties d'un ensemble E à n éléments est 2^n en remarquant qu'on peut associer à chaque partie P de E l'application f de E sur {0,1} ainsi définie :
f(x)=0 si x n'est pas un élément de P
f(x)=1 si x est un élément de P.

Comme Card(E)=n et Card({0,1})=2, on a le résultat, puisque le nombre d'applications d'un ensemble de cardinal p dans un ensemble de cardinal n est n^p.)

Code des exemples : chap_IV_1.zip Miroir 1 , chap_IV_1.zip Miroir 2

Un problème bien connu qui se résout très facilement par un algorithme récursif (et difficilement par un algorithme itératif, comme nous le verrons plus loin) est "les tours de Hanoi". La légende dit que dans un temple de Hanoï, à l'origine du monde, 64 disques de diamètre croissant étaient empilés sur un taquet. Deux autres taquets sont disponibles, qui sont utilisés pour déplacer les disques, la condition étant qu'un disque d'un certain diamètre ne peut pas être placé au dessus d'un disque de diamètre inférieur. Donc, les disques sont toujours empilés dans un certain ordre: les plus grands sont toujours en bas du taquet. La légende dit aussi que des moines sont en train de déplacer les 64 disques vers l'un des deux autres, au rythme de un par seconde et quand ils auront terminé, ce sera la fin du monde.

En faisant un petit calcul rapide, on a 2^64-1 secondes, ce qui correspond à 585 milliards d'années et sachant que l'âge de l'univers est de seulement 15 milliards d'années, on a encore de la marge : ouf ! On l'a échappé belle! :)))

Voyons maintenant la programmation de cet algorithme.

On décide que les disques ont un numéro correspondant à leur diamètre, et que les diamètres vont de 1 à 64.

Nous allons d'abord étudier deux cas concrets de déplacement: comme d'habitude, d'abord on observe, ensuite on programme l'algorithme.

Soit deux disques à déplacer du taquet 1 vers le 3.
Le taquet final est 3, celui initial est 1, donc celui intermédiaire est 2.
Opérations de déplacement :
- disque 1 de taquet 1 vers taquet 2
- disque 2 de taquet 1 vers taquet 3 ---> milieu
- disque 1 de taquet 2 vers taquet 3

Soit trois disques à déplacer du taquet 1 vers le 3.
Le taquet final est 3, celui initial est 1, donc celui intermédiaire est 2.
Maintenant on doit se retrouver avec les deux premiers disques sur le taquet 2, de façon à pouvoir déplacer le disque 3 vers la taquet 3 et ensuite les deux premiers du taquet 2 vers le taquet 3.
Opérations de déplacement :
- disque 1 de taquet 1 vers taquet 3
- disque 2 de taquet 1 vers taquet 2
- disque 1 de taquet 3 vers taquet 2
- disque 3 de taquet 1 vers taquet 3 ---> milieu
- disque 1 de taquet 2 vers taquet 1
- disque 2 de taquet 2 vers taquet 3
- disque 1 de taquet 1 vers taquet 3

En regardant bien les déplacements effectués, on constate les choses suivantes :
- si on a "n" disques à déplacer :
- on déplace "n-1" disques vers le taquet intermédiaire
- on déplace le disque "n" du taquet initial vers le taquet final ---> milieu
- on déplace les "n-1" disques du taquet intermédiaire vers le taquet final

On peut d'ores et déjà en déduire l'algorithme :

procedure TForm1.Button1Click(Sender: TObject);
  procedure hanoi(nb_disques, depart, arrivee: integer);
  var intermediaire: integer;
  begin
    if nb_disques = 1 then
      memo1.lines.add('On déplace un disque de ' +
        inttostr(depart) + ' vers ' + inttostr(arrivee))
    else
    begin
      intermediaire := 6 - depart - arrivee;
      hanoi(nb_disques - 1, depart, intermediaire);
      memo1.lines.add('On déplace un disque de ' +
        inttostr(depart) + ' vers ' + inttostr(arrivee));
      hanoi(nb_disques - 1, intermediaire, arrivee);
    end;
  end;
begin // deplacer 4 disques
  hanoi(4, 1, 2);
end;

Code des exemples : chap_IV_2.zip Miroir 1 , chap_IV_2.zip Miroir 2

Soit la figure suivante :

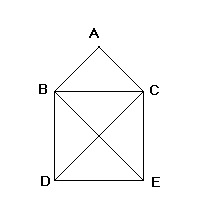
On demande de faire le programme qui trace cette maison en un seul coup, c'est à dire sans "lever le crayon".

Structure des données

Nous devons d'abord représenter la maison en mémoire; on voit que la maison a 5 sommets : A, B, C, D, E. Pour représenter cela, nous allons utiliser un tableau de 2 dimensions qui contiendra 5 lignes et 5 colonnes.

Ensuite, dans ce tableau, on va représenter tous les chemins qu'on peut tracer par un 0 et tous les chemins qu'on ne peut pas tracer (ou qui ont déjà été tracés) par un 1.

On ne peut pas aller de A à A, donc dans le tableau, aux coordonnées (0,0) nous avons un 1; de même pour les autres sommets. Donc la diagonale du tableau (représentant les chemins AA,BB,CC,DD,EE) est mise à 1; en regardant la maison on voit qu'on ne peut pas aller de A à D (donc de D à A non plus) et de A à E (donc de E à A non plus); pour indiquer qu'on ne peut pas (ou plus) aller de A à D, on remplit le tableau en première ligne et quatrième colonne avec 1; pour indiquer qu'on ne peut pas aller de D à A on remplit le tableau en quatrième ligne (car D est le quatrième élément) et première colonne (car A est le premier élément) avec un 1. Idem pour AE.

Analyse de l'algorithme

Faisons une petite analyse du programme:

- on compte les segments à dessiner: il y en a 8 : AB,AC,BC,BD,BE,CD,CE,DE.

- nous allons faire tous les essais possibles sur cette maison; on va donc commencer à la première ligne du tableau et parcourir les colonnes jusqu'à trouver un 0, ce qui indique qu'on peut aller vers ce sommet (par exemple nous sommes à la première ligne, donc au sommet A, et on parcourt les colonnes de cette ligne; on trouve un 0 à la deuxième colonne, donc on peut aller à B; on occupe immédiatement cette case ainsi que celle qui va de B vers A, et on démarre maintenant à la ligne correspondant à B, c'est à dire à la deuxième ligne; la première colonne vide est celle qui correspond à C, étant donné que BA a été rempli ci-dessus; on remplit les cases correspondant aux chemins BC et CB et on démarre à la ligne correspondant à C, c'est à dire la troisième ligne, et ainsi de suite.

- tout ceci se fait par des appels récursifs; la procédure récursive s'appelle "cherche" et elle a 3 paramètres :
-- y: c'est le sommet d'où on part, c'est à dire la ligne en cours dans le tableau
- st : chaîne de caractères qui mémorise le chemin parcouru

Le programme

Voici le programme correspondant :

procedure TForm1.Button1Click(Sender: TObject);
type tab = array[0..4, 0..4] of integer;
 
const t1: tab =
  ((1, 0, 0, 1, 1),
    (0, 1, 0, 0, 0),
    (0, 0, 1, 0, 0),
    (1, 0, 0, 1, 0),
    (1, 0, 0, 0, 1));
 
var t: tab;
 
  procedure cherche(colonne, niveau: integer; st: string);
  var ligne: integer;
  begin
    if niveau = 9 then
      memo1.lines.add(st)
    else
      for ligne := 0 to 4 do
        if t[ligne, colonne] = 0 then
        begin
          st := st + chr(65 + colonne) + chr(65 + ligne) + ' ';
          t[ligne, colonne] := 1; t[colonne, ligne] := 1;
          cherche(ligne, niveau + 1, st);
          t[ligne, colonne] := 0; t[colonne, ligne] := 0;
          delete(st, length(st) - 2, 3);
        end;
  end;
 
  procedure recherche;
  var colonne: integer;
  begin
    memo1.lines.clear;
    move(t1, t, sizeof(t));
    for colonne := 0 to 4 do
      cherche(colonne, 1, '');
  end;
 
begin
  recherche;
end;

Code des exemples : chap_IV_3.zip Miroir 1 , chap_IV_3.zip Miroir 2

Soit un labyrinthe quelconque qui a une entrée et une sortie, ainsi qu'au moins un chemin menant de l'entrée vers la sortie. On veut faire le programme qui trouve l'un de ces chemins. Le principe est simple: nous allons explorer une direction et si elle ne donne aucun résultat, on reprendra une autre direction dans le labyrinthe (une autre branche de l'arbre récursif).

Nous allons étudier quelques détails d'un parcours dans un labyrinthe:
- dans un labyrinthe nous avons quatre directions: nord, est, sud, ouest
- on avance dans le labyrinthe, il faut laisser une trace du passage dans le labyrinthe, car si on a un mur isolé dans le labyrinthe, il ne faut pas tourner à l'infini autour de ce mur
- si à un certain moment on est bloqué, alors on efface le chemin parcouru jusqu'au dernier "carrefour" rencontré dans le labyrinthe et on essaie un autre chemin partant de ce carrefour
- si on est à l'arrivée alors on initialise une variable "trouvé" à true, pour indiquer qu'il ne faut plus effacer la trace laissée derrière, car il faut quand même visualiser le chemin trouvé.

Voyons maintenant l'algorithme :
- l'algorithme sera une procédure qui admet deux paramètres: "ligne" et "colonne"; ils représentent la position en cours
- le point d'appui est atteint quand "ligne" et "colonne" sont égales aux coordonnées du point d'arrivée (la sortie du labyrinthe)
- si on n'est pas au point d'arrivée alors:
1) - on laisse une trace dans le labyrinthe à la position en cours
2) - on affiche le labyrinthe avec la trace
3) - on essaie les quatre directions
- si on peut aller dans une de ces quatre directions (il n'y a pas de mur devant) alors on recommence l'algorithme avec la nouvelle position, celle qui va dans la direction choisie
- si on a essayé toutes les directions alors si "trouvé" est "false" (on n'a pas trouvé la sortie), on efface le chemin.

Remarque: cet algorithme ne trouve pas le meilleur chemin; il trouve simplement un chemin; de plus la longueur du chemin et le temps mis pour le trouver dépend du labyrinthe, de l'emplacement de l'entrée et de la sortie, et du sens qu'on a choisi pour l'exploration des directions d'un carrefour; ici on explore les directions dans l'ordre suivant: nord, ouest, sud, est.

Voici le programme correspondant :

type lab = array[1..15] of string[40];
 
const l: lab = ('$$$$$$ $$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$',
    '$ $$ $         $$$    $$ $$ $$$$ $ $ $$$',
    '$  $ $$$$$$$$$ $$$$$$        $   $     $',
    '$ $$      $$$$        $$ $$$$$ $$$ $$$$$',
    '$ $  $$ $ $    $$$ $$$$$       $   $$$ $',
    '$ $$ $  $$$ $$$$$$$$$  $ $$ $$$$ $$$ $ $',
    '$    $ $$         $ $ $$$$$ $      $   $',
    '$$$$ $ $$ $$$$ $$$$   $$  $$$ $$$$$$ $$$',
    '$$   $    $ $$ $$   $$$$ $$           $$',
    '$$ $$$$$$$$ $$$$$ $$$$ $ $$ $$$$$ $$$$$$',
    '$$ $                     $$            $',
    '$$ $$$ $$ $$$$$ $$$ $$$ $$$$$$ $$ $ $$ $',
    '$$ $$$ $$ $$    $$$  $$ $$ $$$ $$$$$$$$$',
    '$$     $   $$$$     $$                $$',
    '$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ $$$$$$');
 
  dx: array[0..3] of integer = (0, -1, 0, 1);
  dy: array[0..3] of integer = (-1, 0, 1, 0);
 
var t: lab;
  trouve: boolean;
 
procedure tform1.aff_labyrinthe;
var ligne, colonne: integer;
begin
  image1.picture.bitmap.canvas.font.size := 8;
  for ligne := 1 to 15 do
    for colonne := 1 to 40 do
    begin
      case t[ligne][colonne] of
        '$': with image1.picture.bitmap.canvas do
          begin
            brush.Style := bsSolid;
            brush.color := clBlack;
            pen.color := clBlack;
            rectangle((colonne - 1) * 15, (ligne - 1) * 15, colonne * 15, ligne * 15);
          end;
        '*': with image1.picture.bitmap.canvas do
          begin
            brush.Style := bsClear;
            font.color := clBlue;
            textOut((colonne - 1) * 15 + 5, (ligne - 1) * 15 + 2, '*');
          end;
        ' ': with image1.picture.bitmap.canvas do
          begin
            brush.Style := bsSolid;
            brush.color := clWhite;
            pen.color := clWhite;
            rectangle((colonne - 1) * 15, (ligne - 1) * 15, colonne * 15, ligne * 15);
          end;
      end;
    end;
end;
 
procedure tform1.avancer(ligne, colonne: integer);
var i: integer;
begin
  if not trouve then
    if (ligne = 1) and (colonne = 7) then
    begin
      trouve := true;
      edit1.text := 'trouvé';
    end
    else
    begin
      t[ligne][colonne] := '*';
      aff_labyrinthe; image1.refresh;
      for i := 0 to 3 do
        if t[ligne + dy[i]][colonne + dx[i]] = ' ' then
          avancer(ligne + dy[i], colonne + dx[i]);
      if not trouve then
      begin
        t[ligne][colonne] := ' ';
        aff_labyrinthe; image1.refresh;
      end;
    end;
end;
 
procedure TForm1.FormCreate(Sender: TObject);
var tb: tbitmap;
begin
  move(l, t, sizeof(l));
  trouve := false;
  tb := tbitmap.create;
  tb.width := 15 * 40;
  tb.height := 15 * 15; //--- nb d'elems de t; high(t)
  image1.picture.bitmap := tb;
  image1.autosize := true;
  aff_labyrinthe;
end;
 
 
 
procedure TForm1.Button1Click(Sender: TObject);
begin
  edit1.text := 'recherche en cours...'; edit1.refresh;
  avancer(15, 34);
  aff_labyrinthe;
end;

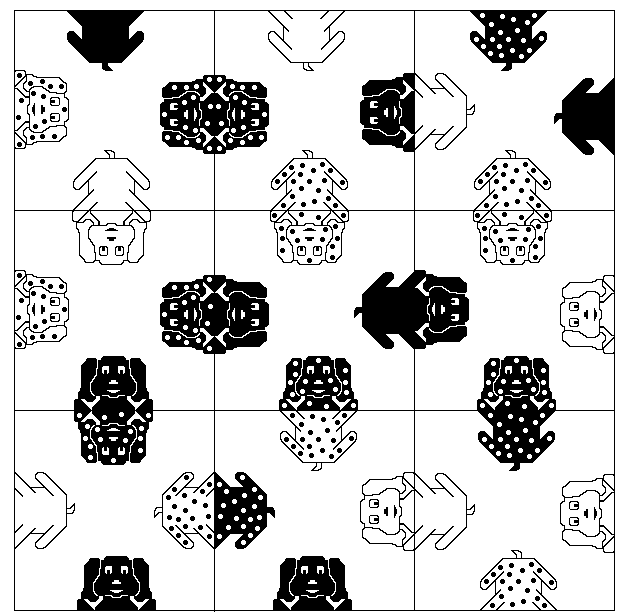
Un problème amusant et pouvant être facilement résolu par l'ordinateur est le problème des petits chiens: on dispose de neuf cartes, chacune contenant quatre têtes ou corps des chiens; le but du jeu est de placer les cartes de manière à avoir réunis la tête et le corps des chiens de même couleur; il y a plusieurs possibilités et comme pour le problème des 8 reines ou du cavalier, nous allons utiliser la récursivité. Les cartes doivent former un carré.

Il est évident qu'il faut former des combinaisons des 9 cartes; pour cela on utilise le programme des anagrammes; on se sert de la deuxième solution, car elle est plus rapide.

procedure combinaisons;
var ch: string;
  l: byte;
 
  procedure EchangeCar(var ch: string; i, j: byte);
  var car: char;
  begin
    if i <> j then
    begin
      car := ch[i];
      ch[i] := ch[j];
      ch[j] := car;
    end
  end;
 
  procedure anagram(ch: string; i: byte);
  var j: byte;
  begin
    if i = l then memo1.lines.add(ch)
    else
      for j := i to l do
      begin
        EchangeCar(ch, i, j);
        Anagram(ch, i + 1);
        EchangeCar(ch, i, j);
      end;
  end;
 
begin
  ch := 'abc'; l := length(ch);
  anagram(ch, 1);
end;

Cette procédure est insuffisante pour résoudre le problème, car les cartes peuvent tourner sur elles-mêmes, quatre fois chacune. Donc pour chaque combinaison obtenue de 9 cartes, il faut faire tourner les cartes et vérifier que la position obtenue crée 12 chiens, sinon il faut essayer une autre position.

Pour vérifier que les chiens sont en position, on fait les tests suivants:
- on pose la première carte
- on pose la deuxième; l'ouest de la deuxième doit correspondre à l'est de la première
- on pose la troisième; l'ouest de la troisième doit correspondre à l'est de la deuxième
- on pose la quatrième; le nord de la quatrième doit correspondre au sud de la première
- on pose la cinquième; le nord de la cinquième doit correspondre au sud de la deuxième et l'ouest de la cinquième doit correspondre à l'est de la quatrième
- on pose la sixième; le nord de la sixième doit correspondre au sud de la troisième et l'ouest de la sixième doit correspondre à l'est de la cinquième
- on pose la septième; le nord de la septième doit correspondre au sud de la quatrième
- on pose la huitième; le nord de la huitième doit correspondre au sud de la cinquième et l'ouest de la huitième doit correspondre à l'est de la septième
- on pose la neuvième; le nord de la neuvième doit correspondre au sud de la sixième et l'ouest de la neuvième doit correspondre à l'est de la huitième

On fait donc une fonction qui vérifie ce qu'il faut en fonction du numéro de la carte passée en paramètre; mais pour vérifier qu'une tête correspond à un corps, on numérote les têtes avec des valeurs positives et les corps correspondants avec des valeurs négatives, de sorte que la somme de la tête et du corps du même chien fasse zéro. En faisant les sommes on peut donc vérifier si une carte est bien placée.

Ensuite pour chaque combinaison obtenue avec les anagrammes, on fait les rotations; la procédure qui s'occupe des rotations fait les étapes suivantes :
- elle a un paramètre qui est le numéro de la carte à tourner
- elle fait une boucle 4 fois pour tourner la carte
- si la carte est bien placée (vérification avec la fonction ci-dessus) alors elle s'appelle elle-même avec un paramètre correspondant au numéro de la carte suivante;
- si le paramètre est 10, alors c'est qu'elle a déjà tourné 9 cartes et qu'elles sont toutes bien placées; c'est donc la solution, et on affiche les 9 cartes.

Le nombre de possibilités (façon d'arranger les cartes) est de (4^9)*9! possibilités. C'est à dire environ 95 milliards, ce qui en fait un bon paquet pour un jeu aussi simple à première vue!

Voici le programme correspondant :

type carte = record
    nord, est, sud, ouest: integer;
  end;
 
const TETE1 = 1; CORPS1 = -1; {--- rouge ---}
  TETE2 = 2; CORPS2 = -2; {--- vert ---}
  TETE3 = 3; CORPS3 = -3; {--- bleu ---}
  TETE4 = 4; CORPS4 = -4; {--- jaune ---}
 
var t: array[1..9] of carte;
  longueur: byte;
  st: string;
  ch: char;
  car: carte;
  nb: longint;
  num: integer;
 
 
//************************************************************************
 
function carte_ok(nb: integer): boolean;
begin
  case nb of
    1: carte_ok := true;
    2: carte_ok := t[1].est + t[2].ouest = 0;
    3: carte_ok := t[2].est + t[3].ouest = 0;
    4: carte_ok := t[1].sud + t[4].nord = 0;
    5: carte_ok := (t[2].sud + t[5].nord = 0) and (t[4].est + t[5].ouest = 0);
    6: carte_ok := (t[3].sud + t[6].nord = 0) and (t[5].est + t[6].ouest = 0);
    7: carte_ok := (t[4].sud + t[7].nord = 0);
    8: carte_ok := (t[5].sud + t[8].nord = 0) and (t[7].est + t[8].ouest = 0);
    9: carte_ok := (t[6].sud + t[9].nord = 0) and (t[8].est + t[9].ouest = 0);
  end;
end;
 
procedure init_carte(var c: carte; nord, est, sud, ouest: integer);
begin
  c.nord := nord; c.est := est; c.sud := sud; c.ouest := ouest;
end;
 
procedure initialisation;
begin
  num := 0;
  st := '123456789';
  init_carte(t[1], CORPS1, TETE4, CORPS2, TETE3);
  init_carte(t[2], TETE2, TETE4, TETE1, TETE3);
  init_carte(t[3], CORPS3, TETE4, CORPS2, TETE1);
  init_carte(t[4], CORPS1, TETE4, TETE1, TETE3);
  init_carte(t[5], CORPS3, TETE2, TETE1, CORPS4);
  init_carte(t[6], TETE2, TETE4, TETE1, TETE3);
  init_carte(t[7], CORPS1, CORPS3, CORPS2, CORPS4);
  init_carte(t[8], TETE4, CORPS3, TETE1, CORPS2);
  init_carte(t[9], TETE2, CORPS3, CORPS2, CORPS4);
end;
 
procedure rotation_droite(var c: carte);
var b: integer;
begin
  b := c.nord;
  c.nord := c.ouest; c.ouest := c.sud; c.sud := c.est; c.est := b;
end;
 
procedure rotations(numero: integer);
var i: integer;
begin
  if numero = 10 then
  begin
    Dessine(Form1.Image1.Canvas, 0, 0, Form1.Image1.Width div 3);
    Screen.Cursor := crDefault;
    inc(num);
    Form1.Label1.Caption := 'Solution ' + IntToStr(num);
    showmessage('Solution ' + IntToStr(num) + ' - Cartes : ' + st);
    Screen.Cursor := crHourGlass;
  end
  else
    for i := 1 to 4 do
    begin
      rotation_droite(t[numero]);
      if carte_ok(numero) then rotations(numero + 1);
    end;
end;
 
procedure anagram(i: byte);
var j: byte;
begin
  if i = 9 then rotations(1)
  else
    for j := i to 9 do
    begin
      car := t[i]; t[i] := t[j]; t[j] := car;
      ch := st[i]; st[i] := st[j]; st[j] := ch;
      anagram(i + 1);
      car := t[i]; t[i] := t[j]; t[j] := car;
      ch := st[i]; st[i] := st[j]; st[j] := ch;
    end
end;

Code des exemples : chap_IV_5.zip Miroir 1 , chap_IV_5.zip Miroir 2

Le jeu du solitaire est un jeu (de réflexion) qui se joue seul; le but du jeu est de ne rester qu'avec un seul pion sur l'échiquier; chaque pion peut sauter par dessus un autre pion à condition que la case d'arrivée soit vide; dans ce cas le pion par dessus lequel on a sauté disparaît. Voici l'échiquier du jeu :

        +-----------+
        ¦ O ¦ O ¦ O ¦         
        +---+---+---¦         
        ¦ O ¦ O ¦ O ¦         
+-------+---+---+---+-------+ 
¦ O ¦ O ¦ O ¦ O ¦ O ¦ O ¦ O ¦ 
+---+---+---+---+---+---+---¦
¦ O ¦ O ¦ O ¦   ¦ O ¦ O ¦ O ¦
+---+---+---+---+---+---+---¦
¦ O ¦ O ¦ O ¦ O ¦ O ¦ O ¦ O ¦
+-------+---+---+---+-------+
        ¦ O ¦ O ¦ O ¦        
        +---+---+---¦        
        ¦ O ¦ O ¦ O ¦         
        +-----------+

Cet échiquier peut se représenter en mémoire par un tableau de 2 dimensions de 7 sur 7; il faut déjà choisir un échiquier de 9 sur 9, pour prévoir une case supplémentaire sur les bords, car si on saute vers l'extérieur, on peut tomber sur n'importe quelle valeur qui se trouve en mémoire; par contre si on a réservé une case, on tombe sur cette case qui aura une valeur indiquant qu'on ne peut pas y sauter. Cette technique sera aussi utilisée dans le jeu d'othello.

Etudions en quelques lignes ce programme :
- on va avoir un échiquier de 9 sur 9, mais en une dimension, donc un tableau linéaire de 81 cases; ceci est fait par souci de rapidité
- pour chaque pion (ou presque) on a quatre directions possibles pour sauter
- on peut sauter si la case jointe est occupée par un pion ET si la case suivante est vide
- une fois qu'on a joué un pion, on fait un appel récursif et on commence la recherche du prochain pion à jouer à partir de la première case

nous allons créer plusieurs procédures :
- l'initialisation de l'échiquier (procédure init_tab;)
- l'affichage de l'échiquier (procédure aff_tab;)
- une fonction pour déterminer quel est le pion qui doit jouer
- la procédure représentant le coeur du programme, la récursivité

Nous allons étudier en détail deux procédures :

la fonction pion_qui_doit_jouer : elle a deux paramètres :
- dernier_pion,qui indique quel est le dernier pion qui a sauté
- last_dir, qui indique quelle est la dernière direction dans la quelle le dernier pion a sauté; si le dernier pion peut sauter dans plusieurs directions et il ne les a pas toutes essayées, alors il les essaie jusqu'au bout, sinon un autre pion est choisi
- pour déterminer quel pion doit jouer, un balayage de l'échiquier a lieu et ce jusqu'à le trouver ou jusqu'à la fin de l'échiquier, à savoir la case numéro 68 dans le tableau, qui correspond au dernier pion de l'échiquier pouvant sauter.

la procédure "joue",qui représente le programme :
- elle n'a pas de paramètres car il faut essayer d'éviter de perdre du temps avec l'empilement et le désempilement de variables pendant l'exécution, vu le nombre élevé de possibilités
- le point d'arrêt est atteint quand on a fait 32 coups, dans ce cas on initialise la variable "trouve" à true et ensuite on ne cherche plus d'autre solution, mais on affiche les sauts et on sort.
- on simule chaque coup par des remplissages du tableau avec des PION et avec des "VIDE", on rappelle la procédure, et ensuite on annule le coup pour essayer une autre possibilité.

Le programme a été testé sur un K6-II 350 et il a calculé 7,4 millions de coups avant de trouver la première solution. Nous avons choisi de l'arrêter délibérément après la première solution, mais vous pouvez le laisser continuer à rechercher d'autres solutions en vous inspirant du programme concernant le saut du cavalier, où les coups sont sauvegardés dans des fichiers distincts.

Voici enfin le programme :

const INCONNU = 5;
  PION = 3;
  VIDE = 0;
 
  d: array[0..3] of integer = (-9, 1, 9, -1);
 
type tab = array[0..80] of byte;
  tab_n = array[1..32] of tab;
 
var t: tab;
  plateaux: tab_n;
  numero_coup: integer;
  nb_coups: longint;
  trouve: boolean;
 
procedure init_tab;
var x, y: integer;
begin
  for x := 0 to 8 do
    for y := 0 to 8 do
      t[x * 9 + y] := INCONNU;
  for y := 1 to 7 do
    for x := 3 to 5 do
    begin
      t[y * 9 + x] := PION;
      t[x * 9 + y] := PION;
    end;
  t[4 * 9 + 4] := VIDE;
end;
 
function pion_qui_doit_jouer(dernier_pion: integer;
  var last_dir: integer): integer;
var i, x, y, k1, k2: integer;
begin
  x := dernier_pion mod 10 - 1;
  y := dernier_pion div 10;
  while (y * 10 + x < 78) do
  begin
    inc(x);
    if (x = 8) then begin x := 0; inc(y); end;
    for i := last_dir to 3 do
    begin
      k1 := y * 9 + x; k2 := d[i];
      if (t[k1] = PION) then
        if (t[k1 + k2] = PION) then
          if (t[k1 + 2 * k2] = VIDE) then
          begin
            last_dir := i;
            pion_qui_doit_jouer := y * 10 + x;
            exit;
          end;
    end;
    last_dir := 0;
  end;
  pion_qui_doit_jouer := 0;
end;
 
procedure joue(numero_coup: integer; var trouve: boolean);
var i, x, y, k1, k2, pion_qui_joue, dernier_pion_qui_a_joue, last_dir, k: integer;
begin
  if (numero_coup = 32) then
  begin
    move(t, plateaux[numero_coup], sizeof(tab));
    trouve := true;
    if Form1.CheckBox1.Checked then Printer.BeginDoc; //Si on veut imprimer
    for k := 1 to 32 do afficher_coup(k);
    if Form1.CheckBox1.Checked then Printer.EndDoc; //Si on veut imprimer
    exit;
  end;
  last_dir := 0;
  dernier_pion_qui_a_joue := 0;
  inc(nb_coups);
  if nb_coups mod 100000 = 0 then
  begin form1.edit1.text := inttostr(nb_coups); form1.edit1.refresh; end;
  repeat
    pion_qui_joue := pion_qui_doit_jouer(dernier_pion_qui_a_joue, last_dir);
    dernier_pion_qui_a_joue := pion_qui_joue;
    if (dernier_pion_qui_a_joue > 0) then
    begin
      move(t, plateaux[numero_coup], sizeof(tab));
      i := last_dir;
      inc(last_dir);
      y := pion_qui_joue div 10;
      x := pion_qui_joue mod 10;
      k1 := y * 9 + x; k2 := d[i];
      t[k1 + 2 * k2] := PION;
      t[k1 + k2] := VIDE;
      t[k1] := VIDE;
      joue(numero_coup + 1, trouve);
      move(plateaux[numero_coup], t, sizeof(tab));
// l'instruction suivante disparaîtra quand on décidera de chercher toutes les solutions
      if trouve then exit;
    end;
  until (pion_qui_joue = 0);
end;

Code des exemples : chap_IV_6.zip Miroir 1 , chap_IV_6.zip Miroir 2

Un problème bien connu par tout le monde est le jeu télévisé "Le compte est bon". Rappelons le principe du jeu pour ceux qui ne le connaissent pas: on tire 6 nombres au hasard parmi les suivants "1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 25, 50, 75, 100" et un autre nombre entre 101 et 999. Il faut trouver le dernier nombre en faisant des opérations mathématiques sur les 6 premiers nombres en ne les utilisant qu'une fois. On reste dans le domaine des entiers naturels (donc positifs). On dispose de quatre opérations : " +, -, *, / ".

Supposons qu'on a seulement deux nombres; les opérations qu'on peut faire sur ces deux nombres sont les suivantes :
"n1 + n2" "n2 + n1"
"n1 - n2" "n2 - n1"
"n1 * n2" "n2 * n1"
"n1 / n2" si n1 est un multiple de n2 "n2 / n1" si n2 est un multiple de n1

On peut tout de suite diviser par 2 le nombre des opérations possibles. On se ramène pour cela au cas où n1 >= n2 :
"n1 + n2" est équivalent à "n2 + n1"
"n2 - n1" n'a pas de sens car cela donnerait un nombre négatif, donc il suffit de considérer "n1-n2"
"n1 * n2" est équivalent à "n2 * n1"
"n1 / n2" n'a de sens que si "n1 >= n2" et si n1 est un multiple de n2

Supposons maintenant qu'on a 3 nombres, par exemple 3, 9, 8. D'après ce qui précède, il faut que les nombres soient triés par ordre décroissant. Pour cela, nous allons les mettre dans un tableau, et on aura : 9, 8, 3. Nous allons travailler tout le long du programme avec seulement des paires de 2 nombres. Ici nous avons trois paires possibles :"9,8", "9,3", "8,3". Pour chacune de ces paires, on fait les quatre opérations et on obtient de nouveaux nombres qu'il faudra combiner avec celui qui reste. Pour mieux comprendre, nous allons détailler les opérations pour ce cas. Il ne faut pas oublier que les nombres sont rangés dans un tableau et que nous allons utiliser ce tableau :

9 + 8 = 17                                                          ¦ 1
    On a un nouveau tableau trié qui contient 2 nombres : 17, 3     ¦
    17 + 3 = 20                                                     ¦ 2
    17 - 3 = 14                                                     ¦ 3
    17 * 3 = 51                                                     ¦ 4
    Division impossible.                                            ¦
9 - 8 = 1                                                           ¦ 5
    On a un nouveau tableau trié qui contient 2 nombres : 3, 1      ¦
    3 + 1 = 4                                                       ¦ 6
    3 - 1 = 2                                                       ¦ 7
    3 * 1 = 3                                                       ¦ 8
    3 / 1 = 3                                                       ¦ 9
9 * 8 = 72                                                          ¦ 10
    On a un nouveau tableau trié qui contient 2 nombres : 72, 3     ¦
    72 + 3 = 75                                                     ¦ 11
    72 - 3 = 69                                                     ¦ 12
    72 * 3 = 216                                                    ¦ 13
    72 / 3 = 24                                                     ¦ 14
Division impossible.                                                ¦

9 + 3 = 12                                                          ¦ 15
    On a un nouveau tableau trié qui contient 2 nombres : 12, 8     ¦
    12 + 8 = 20                                                     ¦ 16
    12 - 8 = 4                                                      ¦ 17
    12 * 8 = 96                                                     ¦ 18
    Division impossible.                                            ¦
9 - 3 = 6                                                           ¦ 19
    On a un nouveau tableau trié qui contient 2 nombres : 8, 6      ¦
    8 + 6 = 14                                                      ¦ 20
    8 - 6 = 2                                                       ¦ 21
    8 * 6 = 48                                                      ¦ 22
    Division impossible.                                            ¦
9 * 3 = 27                                                          ¦ 23
    On a un nouveau tableau trié qui contient 2 nombres : 27, 8     ¦
    27 + 8 = 35                                                     ¦ 24
    27 - 8 = 19                                                     ¦ 25
    27 * 8 = 216                                                    ¦ 26
    Division impossible.                                            ¦
9 / 3 = 3                                                           ¦ 27
    On a un nouveau tableau trié qui contient 2 nombres : 8, 3      ¦
    8 + 3 = 11                                                      ¦ 28
    8 - 3 = 5                                                       ¦ 29
    8 * 3 = 24                                                      ¦ 30
    Division impossible.                                            ¦

8 + 3 = 11                                                          ¦ 31
    On a un nouveau tableau trié qui contient 2 nombres : 11, 9     ¦
    11 + 9 = 20                                                     ¦ 32
    11 - 9 = 2                                                      ¦ 33
    11 * 9 = 99                                                     ¦ 34
    Division impossible.                                            ¦
8 - 3 = 5                                                           ¦ 35
    On a un nouveau tableau trié qui contient 2 nombres : 9, 5      ¦
    9 + 5 = 14                                                      ¦ 36
    9 - 5 = 4                                                       ¦ 37
    9 * 5 = 45                                                      ¦ 38
    Division impossible.                                            ¦
8 * 3 = 24                                                          ¦ 39
    On a un nouveau tableau trié qui contient 2 nombres : 24, 9     ¦
    24 + 9 = 33                                                     ¦ 40
    24 - 9 = 15                                                     ¦ 41
    24 * 9 = 216                                                    ¦ 42
    Division impossible.                                            ¦
Division impossible.                                                ¦

1. on fait un algorithme qui sélectionne une paire
2. on fait une opération sur cette paire
3. si on a trouvé le nombre voulu, on quitte l'algorithme
4. on sauvegarde le tableau courant dans un tableau auxiliaire
5. avec le nombre obtenu après l'opération on obtient un tableau auxiliaire plus petit d'un élément
6. on trie le tableau auxiliaire
7. on fait un appel récursif pour recommencer le raisonnement sur ce tableau
8. si on n'a pas fini les quatre opérations, on boucle sur l'étape 2
9. si on n'a pas fini toutes les paires, on boucle sur l'étape 1

Voyons maintenant quel est le temps d'exécution.

Si toutes les divisions étaient possibles, alors on aurait 60 opérations pour ces 3 nombres, ou trois paires, ce qui n'est pas énorme.

Pour 4 nombres n1, n2, n3, n4 on aurait 6 paires : n1 n2, n1 n3, n1 n4, n2 n3, n2 n4, n3 n4 et, pour chacune de ces paires, on obtiendrait trois sous-paires : par exemple "n1 n2" forme un nombre qui sera combiné avec n3 et avec n4 (c'est le cas ci-dessus, donc 60 combinaisons). Il faut envisager les quatre signes pouvant apparaître entre n1 et n2 donc, pour les trois nombres formés par "n1 n2", "n3", "n4", on a en tout 4*60=240 combinaisons possibles; comme on a six paires à 240 possibilités chacune, on a en tout 1440 possibilités; la croissance est énorme mais en réalité elle est bien inférieure à cause des divisions impossibles et aussi à cause de certaines soustractions, comme nous le verrons par la suite; donc il y a beaucoup de branches de l'arbre récursif qui ne sont pas exploitées.

En faisant le même raisonnement pour 5 nombres on aurait 10 paires à 4 possibilités chacune et à 1440 sous-possibilités, soit 57600 possibilités. Et enfin pour 6 nombres on a 15 paires à 4 possibilités chacune et à 57600 sous-possibilités chacune donc en tout 3.456.000.

En réalité, grâce aux divisions impossibles et grâce aux soustractions qui donnent un reste nul (si on a deux fois 25, alors on a 25 - 25 = 0, inutile de continuer à explorer dans cette direction) on n'explore que 60% des possibilités, c'est à dire environ 2 millions de possibilités.

Pour réduire le temps de réflexion, il faut faire le programme d'une manière différente, car ici on a beaucoup d'opérations qui se répètent comme :
- les opérations 2, 16 et 32, car a+b+c=a+c+b=b+c+a
- les opérations 13, 26 et 42 car a*b*c=a*c*b=b*c*a

Il faut aussi tenir compte de la façon de programmer : étant donné le nombre élevé de combinaisons il faut avoir le moins de procédures possibles, et avec le plus petit nombre de paramètres possible, car pendant la récursivité, le fait d'empiler les variables locales et les paramètres demande beaucoup de temps.

Dans le programme, nous avons dans le tableau "nombres", à l'indice 0, le nombre à trouver (ici 963) et ensuite tous les nombres tirés au hasard. C'est ce tableau qu'il vous faudra modifier pour trouver une solution à un autre problème.

Voici le programme :

type tab = array[0..6] of longint;
 
const signe: string[4] = '+-*/';
  nombres: tab = (963, 25, 5, 4, 3, 3, 1);
 
var trouve, echange: boolean;
  aa: longint;
  ii, jj: integer;
 
procedure operations(var t: tab; max: integer);
var i, j1, j2: integer;
  a: longint;
  t1: tab;
begin
  for i := 1 to 4 do
    for j1 := 1 to max - 1 do
      for j2 := j1 + 1 to max do
      begin
        case i of
          1: a := t[j1] + t[j2];
          2: a := t[j1] - t[j2];
          3: a := t[j1] * t[j2];
          4: begin
              a := t[j1] div t[j2];
              if t[j2] * a <> t[j1] then a := 0;
            end;
        end;
        if a > 0 then
        begin
          if a = t[0] then
          begin
                  //gotoxy(1,8-max);write(t[j1],signe[i],t[j2],'=',a);
            Form1.ListBox1.Items.Add(inttostr(t[j1]) + signe[i] + inttostr(t[j2]) + '=' + inttostr(a));
            trouve := true; exit;
          end;
          move(t, t1, 28);
          t1[j1] := a; t1[j2] := 0;
          repeat
            echange := false;
            for ii := 1 to max - 1 do
              if t1[ii] < t1[ii + 1] then
              begin
                aa := t1[ii]; t1[ii] := t1[ii + 1]; t1[ii + 1] := aa;
                echange := true;
              end;
          until not echange;
          operations(t1, max - 1);
          if trouve then
          begin
                  //gotoxy(1,8-max);write(t[j1],signe[i],t[j2],'=',a);
            Form1.ListBox1.Items.Add(inttostr(t[j1]) + signe[i] + inttostr(t[j2]) + '=' + inttostr(a));
            exit;
          end;
        end;
      end;
end;
 
procedure TForm1.Button1Click(Sender: TObject);
begin
  Screen.Cursor := crHourGlass;
  trouve := false;
  ListBox1.Clear;
  Application.ProcessMessages;
  operations(nombres, 6);
  Screen.Cursor := crDefault;
end;

Code des exemples : chap_IV_7.zip Miroir 1 , chap_IV_7.zip Miroir 2

Les courbes fractales sont des courbes possédant la propriété d'autosimilarité : chacune des parties de la courbe est semblable à n'importe quelle autre. Qu'on s'approche aussi près que l'on veut de la courbe, et on verra toujours la même chose ! Par exemple, le pourtour d'une côte, les arbres et les nuages ont des structures fractales qui peuvent être modélisées mathématiquement.

Nous allons prendre pour exemple la très célèbre courbe en flocon de neige de Von Koch (1904).

Cette courbe est obtenue en partant d'un triangle équilatéral. Sur chaque côté, on construit à l'extérieur du triangle, sur le tiers central, un nouveau triangle équilatéral. En poursuivant à l'infini, on obtient la courbe de Von Koch. Cette courbe n'est pas rectifiable (sa longueur est infinie), elle est continue (elle ne comporte aucun trou) et elle n'est différentiable presque nulle part (il est impossible de construire une tangente en presque chacun de ses points - en mathématiques, on dit qu'un ensemble E possède une propriété P presque partout si on a P pour tous les points de E sauf pour un sous-ensemble dénombrable de points de E -).

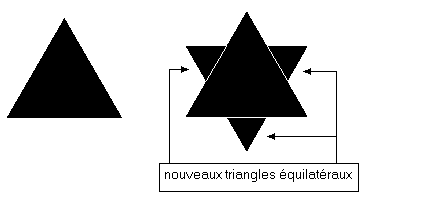
Algorithme du programme « Flocon de Von Koch »

Variables globales :

Ecrx, Ecry : Largeur et hauteur de l'écran
Le tracé est réalisé par deux procédures, la principale étant la procédure Koch.

Définition de la procédure récursive « segment »

Définition de la procédure récursive « segment »

Variables locales :

l : longueur du segment P1P5
x2,x3,x4,y2,y3,y4 : abscisses et ordonnées des points P2, P3, P4.

Calculer la longueur de P1P5 et la stocker dans l

Si la longueur est inférieure à 2 pixels alors tracer le segment P1P5 (en informatique, rien n'est infini !)

Sinon, calculer les coordonnées des points P2 et P4, respectivement barycentres de {(P1,2)(P5,1)} et de {(P1,1)(P5,2)}.

On utilise la formule des barycentres pour couper un segment en trois. Un exemple concret de barycentres est le suivant : on a une poutre avec un poids de 2 kilos à un bout, et un poids de 1 kilo à l'autre bout. La formule du barycentre nous donne le point exact de la poutre où celle-ci est en équilibre.

Dans le programme, comme on l'a dit au début, on dessine sur chaque côté un nouveau triangle équilatéral; mais ce nouveau triangle sera incliné; les triangles qui seront construits sur ses côtés seront aussi inclinés, mais auront un autre angle d'inclinaison, donc nous sommes obligés d'utiliser les formules de rotation dans le plan.

Calculer les coordonnées du point P3, image de P4 par la rotation d'angle 60° et de centre P2

(on montre que x3=x2/2-cos30*y2+x4/2+cos30*y4 et que y3=cos30*x2+y2/2-cos30*x4+y4/2)

Appeler la procédure segment avec les paramètres (x1,y1,x2,y2),
Appeler la procédure segment avec les paramètres (x2,y2,x3,y3),
Appeler la procédure segment avec les paramètres (x3,y3,x4,y4),
Appeler la procédure segment avec les paramètres (x4,y4,x5,y5).

Définition de la procédure Koch

Sans paramètres

Variables locales :

x0, y0 : coordonnées du point de départ du tracé taille : longueur des côtés du triangle initial

Sélectionner une couleur (blanc)
Définir la taille (on prend la moitié de la largeur de l'écran)
Définir x0 pour que le flocon soit centré horizontalement (largeur de l'écran/4)
Définir y0 pour que le flocon soit centré verticalement

Appeler la procédure segment avec les paramètres :
x0, y0, x0+taille, y0
x0+taille, y0, x0+taille/2, y0+cos30*taille
x0+taille/2, y0+cos30*taille, x0, y0

Génération itérative de courbes fractales

Nous allons donner un exemple bien connu de dessin fractal, celui de la courbe de Mandelbrot. Ce dessin est réalisé de façon itérative avec une boucle, à cause de la simplicité de la fonction utilisée; par contre, le dessin du flocon de Von Koch (1904) est récursif.

La courbe de Mandelbrot utilise les nombres complexes, donc le dessin s'effectue dans le plan complexe.

Le programme affiche un dessin qui est l'ensemble des points du plan complexe d'affixe z tels que la suite (|z(n)|) pour n entier naturel, soit convergente, avec : z(0)=z0 et z(n+1)=[z(n)]2+z0.

Vous pouvez initialiser le paramètre "seuil de divergence" à 10, et changer le progressivement de 10 en 10 par exemple. Cela vous permettra de suivre l'évolution de la courbe et des couleurs ("déplacement" progressif).

Vous pouvez aussi changer la variable "profondeur de calcul". Une initialisation à 10 suivi d'une augmentation progressive de 10 en 10 vous permettra de voir la courbe se dessiner à l'écran d'une façon de plus en plus précise.

procedure Dessine;
var large, haut, iimag, ireal, prof: integer; dreal, dimag, lreal, limag, re, im, xx, yy: real;
begin
  large := Form1.Image1.Width;
  haut := Form1.Image1.Height;
  Form1.Image1.Canvas.Brush.Style := bsSolid;
  Form1.Image1.Canvas.Brush.Color := clWhite;
  Form1.Image1.Canvas.Rectangle(0, 0, large, haut);
  dreal := (re_max - re_min) / large;
  dimag := (im_max - im_min) / haut;
  for iimag := 0 to haut - 1 do
    for ireal := 0 to large - 1 do begin
      lreal := re_min + ireal * dreal;
      limag := im_min + iimag * dimag;
      re := lreal;
      im := limag;
      prof := 0;
      repeat
        xx := re * re;
        yy := im * im;
        im := 2 * re * im - limag;
        re := xx - yy - lreal;
        inc(prof);
      until (prof = calprof) or (xx + yy > infini);
      if prof < calprof then begin
        if prof > desprof then Form1.Image1.Canvas.Pixels[ireal, iimag] := color(prof mod 19)
        else if ((prof mod 2) = 0) then Form1.Image1.Canvas.Pixels[ireal, iimag] := color(prof mod 19);
      end;
    end; //next ireal
end;
 
procedure TForm1.Button1Click(Sender: TObject);
begin
  infini := StrToFloat(Edit5.Text); // le nombre que l'on considère comme "infini" (seuil de divergence)
  calprof := StrToInt(Edit6.Text); // profondeur de calcul (nombre d'itérations pour tester la convergence)
  desprof := StrToInt(Edit7.Text); // profondeur de dessin (nb de couleurs utilisées)
  re_min := StrToFloat(Edit1.Text); // x min
  re_max := StrToFloat(Edit2.Text); // x max
  Im_min := StrToFloat(Edit3.Text); // y min
  Im_max := StrToFloat(Edit4.Text); // y max
  if infini <= 0 then infini := 10;
  if calprof <= 0 then calprof := 20;
  if desprof <= 0 then desprof := 10;
  if re_min > re_max then
  begin
    x := re_min;
    re_min := re_max;
    re_max := x;
  end;
  if Im_min > Im_max then
  begin
    x := Im_min;
    Im_min := Im_max;
    Im_max := x;
  end;
  Screen.Cursor := crHourGlass;
  Dessine;
  Screen.Cursor := crDefault;
end;

Code des exemples (Von Koch) : chap_IV_8_a.zip Miroir 1 , chap_IV_8_a.zip Miroir 2

Code des exemples (Mandelbrot) : chap_IV_8_b.zip Miroir 1 , chap_IV_8_b.zip Miroir 2

Il s'agit d'une méthode de tri récursive dont l'efficacité est une fonction croissante du désordre dans le tableau à trier, c'est à dire que plus le tableau est désordonné, plus cette méthode de tri est efficace.

Algorithme du programme QuickSort

Variables globales :

t : le tableau à trier.
Pour l'exemple, nous prendrons t=(3,5,2,4,6,1,4,10), tableau à 8 éléments.

Paramètres :

debut : l'indice du premier élément du tableau à trier,
fin : l'indice du dernier élément du tableau à trier.

Variables locales :

pivot : l'indice de l'élément qui sert de pivot, comme nous allons l'expliquer plus loin,
gauche : l'indice de l'élément en cours de comparaison avec le pivot, situé avant le pivot,
droite : l'indice de l'élément en cours de comparaison avec le pivot, situé après le pivot,
temp : variable tampon juste pour faire l'échange de deux éléments du tableau.

Principe

On appelle la procédure QuickSort en lui passant en paramètres les indices du premier et du dernier élément du tableau à trier : QuickSort(1,8).

On choisit un élément du tableau au hasard. Ce peut être n'importe lequel. Ici, nous choisissons le premier élément du tableau : 3. L'indice de cet élément est appelé le pivot (ici, c'est 1).

On initialise gauche à début (ici, 1) et droite à fin (ici, 8).

La première partie du travail consiste à ranger le tableau de telle sorte que tous les éléments inférieurs à l'élément d'indice pivot se trouvent placés à la gauche de celui-ci (et donc tous les éléments supérieurs à sa droite).

Ceci se fait par comparaisons et échanges successifs :

repeat
  if t[gauche] >= t[droite] then
  begin  //échanger t[droite] et t[gauche]
    temp:=t[gauche];
    t[gauche]:=t[droite];
    t[droite]:=temp;
    pivot:=gauche+droite-pivot; //nouvelle position du pivot
  end;
  if pivot=gauche then dec(droite) else inc(gauche);
until gauche=droite;

Nous comparons d'abord le premier élément du tableau (3) avec le dernier (10).

Comme 3<10, nous ne faisons rien (donc on a encore pivot=gauche) et nous comparons 3 avec l'avant-dernier élément (dec(droite))du tableau (4).

Comme 3<4, nous ne faisons rien (donc on a encore pivot=gauche) et nous comparons 3 avec l'élément d'indice 6 (dec(droite))du tableau (1).

Comme 3>1, nous échangeons les deux éléments afin que 1 se retrouve à gauche de 3 :

3     5     2     4      6      1      4      10
1     5     2     4      6      3      4      10

Comme pivot désigne maintenant un nouvel emplacement (3 est maintenant en sixième position), nous notons celui-ci : pivot:=gauche+droite-pivot;. Ceci est un raccourci élégant pour if pivot=gauche then pivot:=droite else pivot:=gauche;. En effet, pivot est alors égal à droite ou à gauche car pivot était égal avant à gauche ou à droite.

pivot étant maintenant égal à droite, nous augmentons gauche d'une unité (inc(gauche)) car 1 est désormais placé à gauche de 3 et nous n'avons plus à nous en occuper. A ce stade, gauche=2, pivot=droite=6. Comme gauche est différent de droite, nous continuons.

Comme 5>3, nous échangeons les deux éléments afin que 5 se retrouve à droite de 3 :

1     5     2      4      6      3      4      10
1     3     2      4      6      5      4      10

Comme pivot désigne maintenant un nouvel emplacement (3 est maintenant en deuxième position), nous notons celui-ci : pivot:=gauche+droite-pivot=gauche=2;.

pivot étant maintenant égal à gauche, nous diminuons droite d'une unité (dec(droite)) car 5 est désormais placé à droite de 3 et nous n'avons plus à nous en occuper. A ce stade, gauche=pivot=2, droite=5. Comme gauche est différent de droite, nous continuons.

Comme 3<6, nous ne faisons rien (donc on a encore pivot=gauche) et nous comparons 3 avec l'élément d'indice 4 (dec(droite))du tableau (4).

Comme 3<4, nous ne faisons rien (donc on a encore pivot=gauche) et nous comparons 3 avec l'élément d'indice 3 (dec(droite))du tableau (2).

Comme 3>2, nous échangeons les deux éléments afin que 2 se retrouve à gauche de 3 :

1     3     2      4      6      5      4      10
1     2     3      4      6      5      4      10

Comme pivot désigne maintenant un nouvel emplacement (3 est maintenant en troisième position), nous notons celui-ci : pivot:=gauche+droite-pivot=droite=3;.

pivot étant maintenant égal à droite, nous augmentons gauche d'une unité (inc(gauche)) car 2 est désormais placé à gauche de 3 et nous n'avons plus à nous en occuper. A ce stade, gauche=3, pivot=droite=3. Comme gauche est égal à droite, nous sortons de la boucle repeat/until et nous avons terminé la première phase du travail.

Le tableau est maintenant divisé en deux parties par l'élément d'indice pivot (3) :

     1     2
et :
     4     6      5      4      10

Les éléments de la partie gauche sont tous inférieurs à 3 et ceux de la partie droite lui sont tous supérieurs. C'est le but que nous nous étions fixé.

Il ne reste plus qu'à laisser opérer la magie de la récursivité, c'est à dire à appeler à nouveau (récursivement) notre procédure QuickSort pour chacun des deux sous-tableaux !

Comme debut<gauche-1 (1<3-1), c'est ce que nous nous empressons de faire avec QuickSort(1,2), et avec QuickSort(4,8), puisque fin>droite+1 (8>3+1) !

L'appel à QuickSort sur la partie gauche n'amènera pas de modification puisque le sous-tableau gauche est déjà trié.

L'appel à QuickSort sur la partie droite conduira à deux échanges pour placer le 6 avant le 10, qui suffiront à terminer le tri. En cours de chemin, il y aura deux sous-appels (inutiles !) à QuickSort qui n'amèneront donc pas de modifications.

Code de la procédure (récursive) QuickSort

procedure QuickSort(debut, fin: integer);
var pivot, gauche, droite, temp: integer;
begin
  pivot := debut;
  gauche := debut;
  droite := fin;
  repeat
    if t[gauche] >= t[droite] then
    begin //échanger t[droite] et t[gauche]
      temp := t[gauche];
      t[gauche] := t[droite];
      t[droite] := temp;
      pivot := gauche + droite - pivot; //nouvelle position du pivot
                     //pivot est alors égal à droite ou à gauche car pivot était égal
                     //avant à gauche ou à droite.
                     //c'est un raccourci élégant pour "if pivot=gauche then pivot:=droite else pivot:=gauche;"
    end;
    if pivot = gauche then dec(droite) else inc(gauche);
  until gauche = droite;
  if debut < gauche - 1 then QuickSort(debut, gauche - 1); //appel récursif sur la partie gauche
  if fin > droite + 1 then QuickSort(droite + 1, fin); //appel récursif sur la partie droite
end;

Code des exemples : chap_IV_9.zip Miroir 1 , chap_IV_9.zip Miroir 2

Un petit problème intéressant concernant les nombres est la décomposition du carré d'un nombre en une somme de carrés de nombres différents tous plus petits que le premier.

exemple : soit le nombre 11. 11^2=121. Il faut décomposer le nombre 121 en une somme de carrés de nombres distincts plus petits que 11. Plusieurs solutions se présentent à chaque fois, et plus le nombre initial est grand, plus il y a de solutions. Voici deux décompositions pour le carré de 11 (une autre solution vous sera donnée par l'algorithme) :
121=100+16+4+1=102+42+22+12
121=81+36+4=92+62+22

Nous allons d'abord étudier sur le cas concret présenté ci-dessus l'approche à effectuer.

Notre nombre est 11. On doit donc prendre un par un tous les nombres inférieurs à 11, soustraire leur carré de 121, extraire la racine carrée (éventuellement majorée si le résultat n'est pas entier) du résultat et recommencer.

exemple :

On doit trouver 121 avec la somme des carrés de nombres plus petits que 11.

1. On prend 10 et on l'élève au carré : 10*10=100.
2. On soustrait : 121-100=21.
3. On extrait la racine carrée de 21 et on obtient 4,6; on majore le résultat par 5.

appel récursif :

On doit maintenant trouver le résultat du b0) avec la somme des carrés de nombres plus petits que 5.

1. 1 On prend 4 et on l'élève au carré: 4*4=16.
2. 1 On soustrait : 21-16=5.
3. 1 On extrait la racine carrée de 5 et on obtient 2,2; on majore le résultat pour obtenir 3.

appel récursif :

On doit maintenant trouver le résultat du b1) avec la somme des carrés de nombres plus petits que 3.

1. 2 On prend 2 et on l'élève au carré: 2*2=4.
2. 2 On soustrait : 5-4=1.
3. 2 On extrait la racine carrée de 1 et on obtient 1; on ne majore pas le résultat car il est entier.

appel récursif :

On doit maintenant trouver le résultat du b2) avec la somme des carrés de nombres plus petits ou égaux à 1.

1. 3 On prend 1 et on l'élève au carré: 1*1=1
2. 3 On soustrait: 1-1=0

1. 2 On prend 1 et on l'élève au carré: 1*1=1.
2. 2 On soustrait: 5-1=4.
3. 2 On extrait la racine carrée de 4 et on obtient 2; on ne majore pas le résultat car il est entier.

1. 1 On prend 3 et on l'élève au carré: 3*3=9.
2. 1 On soustrait 21-9=12.
3. 1 On extrait la racine carrée de 12 et on obtient 3,5; on majore le résultat pour obtenir 4.

appel récursif :

On doit maintenant trouver le résultat du b1) avec la somme des carrés de nombres plus petits que 4.

1. 2 On prend 3 et on l'élève au carré: 3*3=9.
2. 2 On soustrait : 12-9=3.
3. 2 On extrait la racine carrée de 3 et on obtient 1,7; on majore le résultat par 2.

appel récursif :

On doit maintenant trouver le résultat du b) avec la somme des carrés de nombres plus petits ou égaux à 1.

... et ainsi de suite.

Nous devons donc créer une fonction qui extrait la racine carrée d'un nombre et qui la majore lorsque le résultat n'est pas entier.

function racine_majoree(carre: integer): integer;
var a: integer;
begin
  a := round(sqrt(carre));
  if a * a < carre then inc(a);
  racine_majoree := a;
end;

Nous devons utiliser ensuite un tableau d'entiers dans lequel nous allons accumuler les valeurs décroissantes dont la somme des carrés donne le nombre cherché. Nous allons ensuite les concaténer tous dans une chaîne, de façon à pouvoir les afficher.

t: array[0..50] of integer;
s: string;

• a_trouver : le nombre à trouver qui est au début un carré, ensuite une différence de carrés. Ce nombre diminue au fur et à mesure qu'on descend dans la récursion.
• nb : le nombre à partir duquel on va chercher les carrés. Ainsi, si le nombre initial est 11, ce paramètre de la procédure sera 10. Il est calculé dans cette procédure avant chaque appel récursif.
• niveau : une variable qui sert d'indice pour le tableau dans lequel on accumule les nombres qui constitueront la solution finale
• exacte : une variable booléenne qui indique si la précédente racine carrée extraite était entière ou si elle avait été majorée. Si elle avait été majorée, alors on doit décrémenter nb.

Pendant la recherche et l'accumulation des nombres dans le tableau, on doit aussi vérifier que chaque nombre ajouté est plus petit que son prédécesseur, sinon on obtient n'importe quel nombre comme une somme de nombres 1 (qui est lui-même le carré de 1, donc le résultat est bien une somme de carrés !).

L'algorithme est le suivant :

procedure cherche(a_trouver, nb, niveau: integer; exacte: boolean);
var bool: boolean;
  rac, diff, carre, i, j: integer;
begin
  if not exacte then dec(nb);
  for i := nb downto 1 do
  begin
    carre := i * i;
    diff := a_trouver - carre;
    if (diff = 0) and (i < t[niveau - 1]) then
    begin
      s := '';
      for j := 1 to niveau - 1 do s := s + inttostr(t[j] * t[j]) + '+';
      s := s + inttostr(carre) + '=' + inttostr(nb1 * nb1);
      memo1.lines.add(s);
    end
    else
    begin
      rac := racine_majoree(diff);
      t[niveau] := i;
      bool := (rac * rac = diff);
      if (i < t[niveau - 1]) then //--- on s'assure que les nombres sont distincts
        cherche(diff, rac, niveau + 1, bool);
    end;
  end;
end;

Code des exemples : chap_IV_10.zip Miroir 1 , chap_IV_10.zip Miroir 2

On dispose d'un seau d'eau vide et de bouteilles de tailles différentes qui sont remplies d'eau. Quelle est la combinaison de bouteilles dont l'eau, une fois versée dans le seau, le remplit au maximum? Le problème peut être transposé à des chansons qui doivent remplir au mieux une cassette audio. Dans l'exemple suivant on a pris arbitrairement un seau dont le volume est de 1885 et 5 bouteilles dont les volumes sont dans le tableau t.

Une solution à ce problème est donnée en utilisant le programme qui faisait des anagrammes; il suffit de chercher la combinaison de bouteilles qui remplit au mieux un volume donné.

const t: array[1..5] of integer = (250, 370, 451, 749, 634);
  max: longint = 1885;
 
var temoin: string;
  difference: longint;
  nb_bouteilles: integer;
 
procedure anagrammes(st: string; nb1, nb2: byte; result: integer);
var i: byte;
begin
  for i := nb1 to nb2 do
    if difference = 0 then exit else
      if nb2 < nb_bouteilles then anagrammes(st + chr(64 + i), i + 1, nb2 + 1, result + t[i])
      else
        if (max - result - t[i] < difference) and (max - result - t[i] >= 0) then
        begin
          temoin := st + chr(64 + i);
          difference := max - result - t[i];
          form1.memo1.lines.add('meilleure combinaison pour l''instant : ' +
            temoin + ';reste à remplir:  ' + inttostr(difference) + ' litres');
        end;
end;
 
procedure recherche;
var i: integer;
  s: string;
begin
  nb_bouteilles := high(t);
  form1.memo1.lines.add('Vous disposez de ' + inttostr(nb_bouteilles) + ' bouteilles.');
  form1.memo1.lines.add('Ces bouteilles sont numérotées avec des lettres.');
  form1.memo1.lines.add('Leurs volumes respectifs sont :');
  for i := 1 to nb_bouteilles do
    form1.memo1.lines.add(chr(64 + i) + '=' + inttostr(t[i]) + ' litres');
  form1.memo1.lines.add('On doit remplir un volume de ' + inttostr(max) + ' litres.');
  for i := 1 to nb_bouteilles do anagrammes('', 1, i, 0);
  form1.memo1.lines.add('');
  s := 'bouteilles = ' + temoin + '; partie remplie = ' + inttostr(max - difference) + ' litres';
  form1.memo1.lines.add(s);
  s := 'reste à remplir = ' + inttostr(difference) + ' litres; maximum remplissable = ' + inttostr(max) + ' litres';
  form1.memo1.lines.add(s);
  s := 'pourcentage de remplissage : ' + inttostr(100 - round(difference * 100 / max)) + ' %';
  form1.memo1.lines.add(s);
end;
 
procedure TForm1.Button1Click(Sender: TObject);
begin
  difference := max; temoin := '';
  recherche;
end;

Code des exemples : chap_IV_11.zip Miroir 1 , chap_IV_11.zip Miroir 2

Le programme suivant cherche le chemin le plus court pour aller d'une station de métro à une autre. Il fonctionne avec le métro parisien, mais il peut être bien évidemment être utilisé avec n'importe quel autre réseau.

Dans un premier temps, nous allons appliquer cet algorithme à un réseau très simple, avec quelques stations. C'est le programme qui suit. Le programme réel, avec toutes les stations du métro et les optimisations, est à télécharger.

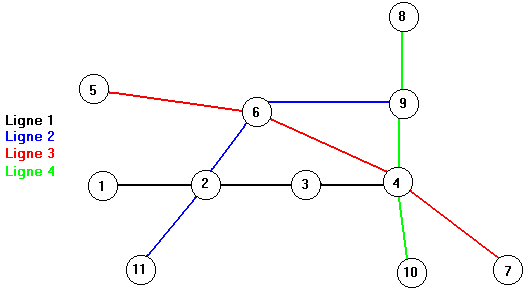
Nous allons d'abord définir le type "arc", représentant le chemin entre deux stations; il contient le numéro de la station de départ, le numéro de la station d'arrivée et un indicateur qui nous dit si un arc a déjà été emprunté (afin d'éviter les boucles) :

arc = record
  depart, arrivee: integer;
  parcouru: boolean;
end;

Nous allons ensuite entrer les arcs correspondants :

procedure init_arcs;
begin
  t[1].depart := 1; t[1].arrivee := 2; t[1].parcouru := false;
  t[2].depart := 2; t[2].arrivee := 1; t[2].parcouru := false;
  t[3].depart := 2; t[3].arrivee := 3; t[3].parcouru := false;
  t[4].depart := 2; t[4].arrivee := 6; t[4].parcouru := false;
  t[5].depart := 2; t[5].arrivee := 11; t[5].parcouru := false;
  t[6].depart := 3; t[6].arrivee := 2; t[6].parcouru := false;
  t[7].depart := 3; t[7].arrivee := 4; t[7].parcouru := false;
  t[8].depart := 4; t[8].arrivee := 3; t[8].parcouru := false;
  t[9].depart := 6; t[9].arrivee := 4; t[9].parcouru := false;
  t[10].depart := 4; t[10].arrivee := 7; t[10].parcouru := false;
  t[11].depart := 4; t[11].arrivee := 9; t[11].parcouru := false;
  t[12].depart := 4; t[12].arrivee := 10; t[12].parcouru := false;
  t[13].depart := 5; t[13].arrivee := 6; t[13].parcouru := false;
  t[14].depart := 6; t[14].arrivee := 2; t[14].parcouru := false;
  t[15].depart := 6; t[15].arrivee := 4; t[15].parcouru := false;
  t[16].depart := 6; t[16].arrivee := 5; t[16].parcouru := false;
  t[17].depart := 6; t[17].arrivee := 9; t[17].parcouru := false;
  t[18].depart := 7; t[18].arrivee := 4; t[18].parcouru := false;
  t[19].depart := 8; t[19].arrivee := 9; t[19].parcouru := false;
  t[20].depart := 9; t[20].arrivee := 4; t[20].parcouru := false;
  t[21].depart := 9; t[21].arrivee := 6; t[21].parcouru := false;
  t[22].depart := 9; t[22].arrivee := 8; t[22].parcouru := false;
  t[23].depart := 10; t[23].arrivee := 4; t[23].parcouru := false;
  t[24].depart := 11; t[24].arrivee := 2; t[24].parcouru := false;
  min_stations := 10000; // initialisé à plus l'infini
end;

On doit faire ensuite une procédure qui pour un station donnée cherche toutes les stations qui sont à une distance de 1 de celle-ci. Ainsi, dans le dessin précédent, les stations situées à une distance de 1 de la station numéro 4 sont les suivantes: 3,6,9,7 et 10.

procedure trouve_partantes(depart: integer);
var i: integer;
begin
  nb_partantes := 0;
  for i := 1 to 24 do
  begin
    if t[i].depart = depart then
    begin
      inc(nb_partantes);
      partantes[nb_partantes] := i; // valeur de "i" utilisée dans "trouver"
    end;
  end;
end;

Ensuite, pendant le parcours du graphe (afin de chercher le chemin le plus court) si on a emprunté un arc, on doit le marquer; de cette façon, on empêche le programme de boucler. Inversement, si on a pris un chemin et qu'il s'est révélé infructueux, on doit faire demi-tour (en réalité on monte d'un niveau dans la pile de la procédure récursive) et marquer l'arc comme n'étant pas emprunté. Ce qui nous donne :

procedure marquer_arc(depart, arrivee: integer; marque: boolean);
var i: integer;
begin
  for i := 1 to 23 do
  begin
    if (t[i].depart = depart) and (t[i].arrivee = arrivee) then
      t[i].parcouru := marque;
    if (t[i].depart = arrivee) and (t[i].arrivee = depart) then
      t[i].parcouru := marque;
  end;
end;

Il nous reste maintenant à faire la fonction de recherche du plus court chemin entre deux stations. Cette fonction a les paramètres suivants :
- départ et arrivée, indiquant les numéros de stations
- nb_stations: variable indiquant (à un niveau n de la récursivité) le nombre de stations parcourues.
- liste: une chaîne de caractères, dans laquelle on mémorise les numéros des stations.

La programmation de cette fonction se fait de la manière suivante :
- pour chaque chemin trouvé, on mémorise le nombre de stations dans une variable, appelée "min_stations". De cette façon, on est sûr que la longueur des chemins trouvés va aller en diminuant.
- si on n'a pas trouvé le chemin (c'est à dire "départ<>arrivée") alors pour la station en cours (c'est à dire "départ") on mémorise toutes les stations partantes, et on les essaye une par une. Grâce à la récursivité, pour chacune de ces stations partantes on mémorise leur propres stations partantes et on les essaie (descente récursive et exploration de tous les chemins).

Il faut donc marquer l'arc emprunté, essayer la première station et si elle a échoué alors effacer l'arc emprunté et prendre la deuxième station; et ainsi de suite.

function trouver(depart, arrivee, nb_stations: integer; liste: string): boolean;
var i: integer;
  partantes1: tp;
  nb_partantes1: integer;
begin
  if depart = arrivee then
  begin
    trouver := true;
    if nb_stations <= min_stations then
    begin
      min_stations := nb_stations;
      form1.memo1.lines.add('Nouveau plus petit chemin :');
      form1.memo1.lines.add(inttostr(nb_stations) + ' stations.');
      form1.memo1.lines.add(liste);
      form1.memo1.lines.add('=============================');
    end;
  end
  else
  begin
    trouve_partantes(depart);
    move(partantes, partantes1, sizeof(tp));
    nb_partantes1 := nb_partantes;
    for i := 1 to nb_partantes1 do
      if t[partantes1[i]].parcouru = false then
      begin
        marquer_arc(depart, t[partantes1[i]].arrivee, true);
        trouver := trouver(t[partantes1[i]].arrivee, arrivee,
          nb_stations + 1, liste + ',' + inttostr(t[partantes1[i]].arrivee));
        marquer_arc(t[partantes1[i]].arrivee, depart, false);
      end;
  end;
end;

On n'a plus qu'à appeler la fonction ci-dessus :

procedure TForm1.Button1Click(Sender: TObject);
begin
  init_arcs;
  trouver(5, // station départ
    7, // station arrivée
    0, // stations parcourues
    '5'); // chemin parcouru
end;

Passons maintenant dans le cas réel, c'est à dire environ 300 stations de métro.

Là, prendre tous les chemins peut s'avérer extrêmement long. C'est pour cette raison qu'on introduit un nombre maximal de changements autorisés.

L'algorithme prend les chemins dans l'ordre de leur introduction en mémoire. Si on lui laisse un nombre maximal de 5 changements par exemple, alors le nombre de chemins possibles sera beaucoup plus grand que si on lui impose seulement 2 changements. C'est donc à vous de choisir et de faire des essais, pour déterminer le trajet et le temps de trajet qui vous convient le mieux.

Le programme fonctionnel des stations de métro est à télécharger.

On peut ensuite modifier l'algorithme de recherche en ne lui donnant que les stations qui se trouvent à un croisement, de cette façon la recherche sera encore plus rapide. Actuellement le programme met de 1 seconde à quelques minutes pour trouver un chemin optimal, mais l'affichage des solutions est progressif

Code des exemples : chap_IV_12.zip Miroir 1 , chap_IV_12.zip Miroir 2

Introduction

De nos jours, de nombreux programmes doivent convertir des sommes en lettres. Nous vous présentons ici un programme qui traduit un nombre entier (une suite de chiffres) quelconque en son expression littérale correspondante en français (exemple : 314 = « trois cent quatorze »). Le programme traite les nombres décimaux en traitant de façon distincte la partie entière et celle décimale, puis concatène ensuite les deux. Il peut être utilisé par exemple dans les logiciels qui impriment des chèques.

Nous allons découvrir quels sont les problèmes liés à la langue française qui peuvent apparaître dans ce programme.

Façon d'écrire un nombre en toutes lettres en français

Problèmes d'écriture
Nous allons étudier un peu les différents cas qui peuvent se présenter.

Unités :
Le chiffre des unités ne pose aucun problème, chaque chiffre a un correspondant littéral :
0= « zéro » , 1 = « un », 2= « deux » et ainsi de suite.

Dizaines :
Par contre, dès qu'on arrive aux dizaines, les choses se compliquent car la façon d'écrire et de prononcer les nombres varie selon le chiffre utilisé. Ainsi on dit « onze » au lieu de « dix et un » (par contre on dit « vingt et un ») , on dit « douze » au lieu de « dix-deux » (par contre on dit « vingt-deux ») et ainsi de suite jusqu'à seize. Mais à partir de là on dit bien « dix-sept » (de même que « vingt-sept »), « dix-huit », etc.

Le cas du mot « et » (conjonction de coordination)
Noter le fait qu'on rajoute le mot « et » pour le chiffre « 1 » (vingt ET un, trente ET un, quarante ET un, cinquante ET un, soixante ET un, soixante ET onze) mais pas pour les autres dizaines.

D'autres particularités concernent le soixante-dix, quatre-vingt, quatre-vingt-dix. Ces cas sont spécifiques au français utilisé en France, qui est différent de celui utilisé en Suisse, où il y a une façon bien plus simple de dire ces nombres : septante, huitante, nonante (et c'est très logique ! ) , ou en Belgique qui utilise « septante, octante, nonante »

On constate qu'on a trois cas où on utilise « onze » (11,71,91) et 7 cas où on utilise « un » (1,21,31,41,51,61,81).

En plus de cela, il y a les cas des mots « vingt » et « quatre-vingt »:

VINGT
1. L'adjectif numéral prend la marque du pluriel s'il est multiplié par un nombre et s'il n'est pas suivi d'un autre adjectif de nombre.
Exemple : Quatre-vingts feuilles, quatre-vingt-huit francs.
Attention aux mots million, milliard qui ne sont pas des adjectifs numéraux, mais des noms.
Exemple : Quatre-vingts millions.
Précédé de cent ou de mille, l'adjectif numéral est toujours invariable.
Exemple : Cent vingt personnes.
2. Dans les adjectifs numéraux composés, le trait d'union s'emploie seulement entre les éléments qui sont l'un et l'autre inférieurs à cent, sauf si ces éléments sont joints par la conjonction « et ».
Exemple : Vingt et un. Vingt-cinq.

QUATRE-VINGT(s) adj. et n. m. · Adjectif numéral cardinal. Quatre fois vingt.
Il a quatre-vingts ans, elle a quatre-vingt-deux ans.
Note.- L'adjectif numéral cardinal s'écrit avec un « s » s'il est multiplié par un nombre et s'il n'est pas suivi d'un autre adjectif numéral.
· Adjectif numéral ordinal invariable.
Exemple : Quatre-vingtième. La page quatre-vingt. En mil neuf cent quatre-vingt.
· Nom masculin invariable.
Exemple : Des quatre-vingt en lettres lumineuses.

1. Attention aux nombres composés des mots million, milliard qui ne sont pas des adjectifs numéraux, mais des noms et qui permettent donc la marque du pluriel à vingt si l'adjectif numéral est multiplié par un nombre. Exemple : Quatre-vingts millions de francs.
2. Après l'adjectif numéral, la conjonction « et » ne s'emploie pas devant « un » , contrairement à « trente et un », « quarante et un »... Exemple : Quatre-vingt-un citrons, quatre-vingt-une tomates.
3. Les adjectifs numéraux composés de quatre-vingt s'écrivent avec des traits d'union. Exemples : Quatre-vingt-deux, quatre-vingt-trois, quatre-vingt-dix, quatre-vingt-onze, quatre-vingt-dix-sept.

Centaines :
Pour les centaines c'est plus simple, car le seul cas particulier qui existe est celui de « cent » (on ne dit pas « un cent » mais « cent » tout court), tous les autres multiples de 100 ayant le nom du chiffre devant : « deux cent » , « trois cent »…
Le problème du « s » (utilisé dans certains cas pour le pluriel de « cent ») est traité ici.
L'adjectif « cent » :
- il prend un « s » quand il est multiplié par un autre nombre et qu'il termine l'adjectif numéral.
exemple : J'ai lu sept cents pages.
- il est invariable quand il n'est pas multiplié par un autre nombre
Exemple : Il a lu cent pages.
- il est invariable quand il est suivi d'un autre nombre.
Exemple : Elle a écrit trois cent vingt-sept pages.
- devant millier, million, milliard , il s'accorde quand il n'est pas suivi d'un nom de nombre.
Exemple : Quatre cents millions de francs.

Le reste
Au delà de mille, million, milliard les nombres s'écrivent de la même façon, et ils sont lus par groupes de 3 chiffres.
On voit donc qu'il est important de connaître le nombre de chiffres des nombres pour bien les prononcer. Paradoxalement, il est clair que si la lecture d'un nombre se fait bien (tout comme un mot) de gauche à droite, sa prononciation dépend fortement des groupements de trois chiffres que l'on peut opérer à partir de la droite cette fois. D'où l'intérêt d'un caractère séparateur de milliers (caractères « espace » ou « . ») pour faciliter cette lecture dans la vie courante (exemple : 1.325.240), comme on le voit dans les pays anglo-saxons.

Les structures utilisées dans le programme

Nous allons créer un tableau comportant les nombres de un à dix-neuf, qui seront utilisés trois fois :
- pour tout nombre compris dans l'intervalle 1..19
- pour tout nombre compris dans l'intervalle 61..79
- pour tout nombre compris dans l'intervalle 81..99

A noter que parmi ces trois cas, seuls les nombres 61 et 71 se voient attribuer le mot « ET » entre le chiffre des dizaines et celui des unités.

On crée ensuite un tableau des dizaines qui contient les nombres vingt, trente, quarante, cinquante, soixante, soixante, quatre-vingt, quatre-vingt.

Remarque : 'soixante' et 'quatre-vingt' apparaissent deux fois, une fois en propre et l'autre pour former les cas spéciaux des intervalles 70..79 et 90..99.

On crée ensuite un tableau qui contient les unités restantes : mille, million, milliard,…

Nous allons supposer que le nombre saisi au clavier peut aussi contenir deux décimales.

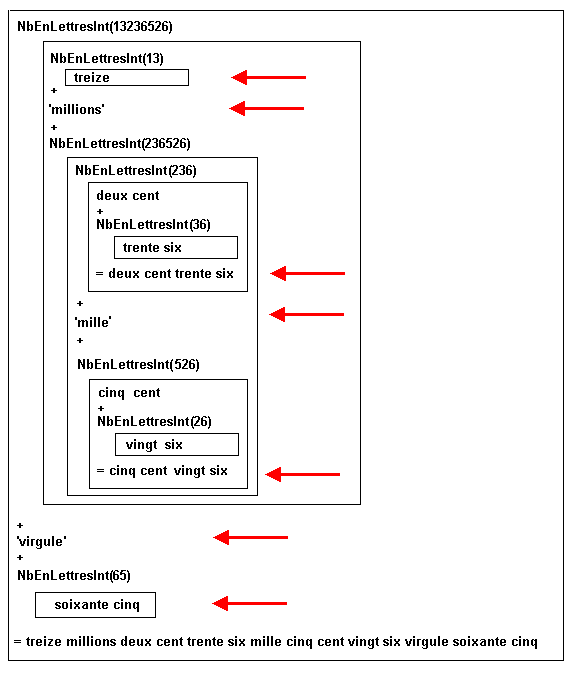
Le principe récursif fait qu'on sait qu'un nombre à évaluer est égal à l'évaluation de sa partie principale (groupe de trois chiffres maximum) plus l'évaluation du reste

13.236.526,65 = évaluation de '13' + évaluation de '236.526,65'
   236.526,65 = évaluation de '236' + évaluation de '526,65'
       526,65 = évaluation de '526' + 'virgule' + évaluation de '65'
           65 = évaluation de '60' + évaluation de '5' = 
                                   'soixante' + 'cinq' = 'soixante cinq' ;
       526    = évaluation de '500' + évaluation de '26'
        26    = évaluation de '20' + évaluation de '6' = 'vingt' + 'six' = 'vingt six'
                évaluation de '500' = 'cinq' + 'cent' = 'cinq cent' ;
             et ainsi de suite…

ensuite on n'a plus qu'à concaténer les résultats des différentes évaluations pour obtenir le résultat final.

La seule difficulté consiste à déterminer la partie principale d'un nombre. Nous avons en effet l'habitude de lire les nombres de gauche à droite en isolant les groupes de trois chiffres (millions, milliers) puis à l'intérieur les centaines, dizaines et unités. La seule difficulté pratique du langage consiste à déterminer le rang maximal du nombre, c'est-à-dire si le premier groupe à partir de la gauche est celui des milliards, millions, milliers , … mais pour cela, les yeux comptent les chiffres à partir de la droite !

Cette petite contradiction levée, l'algorithme que l'esprit suit intuitivement consiste à évaluer le groupe de trois chiffres le plus à gauche, puis à répéter l'opération en ne considérant que les chiffres restants à droite : cette méthode d'évaluation / séparation est caractéristique d'un processus récursif ! Seul point négatif, les résultats intermédiaires sont moins significatifs (voire même inexistants) que dans la méthode itérative et rendent difficile la gestion des exceptions du pluriel, etc …

Techniquement, l'algorithme va essayer de déterminer le groupe maximal à chaque étape et va analyser son coefficient, le traduire, puis relancer la fonction pour les chiffres restants : cela garantit qu'un groupe de trois chiffres tels que les millions ne seront évalués qu'une fois, car au prochain appel récursif un groupe de milliers (au plus) sera analysé , … , jusqu'à ce que l'on arrive finalement aux unités finales (ou des décimales) du nombre, terme de la récursivité.

Les spécificités de l'algorithme

Avant d'appeler la procédure récursive, on s'assurera tout d'abord que le nombre ne contient pas une virgule, auquel cas on évaluera d'abord sa partie entière, puis ensuite celle décimale (arrondie à deux décimales) , que l'on collera à la suite de la première et du mot « virgule » .

L'étape de base consiste à récupérer la longueur du nombre, afin de prendre la partie principale et l'évaluer. On fera ensuite un appel récursif et on collera cette évaluation à l'évaluation du reste.

Nous avons créé un tableau contenant l'expression littérale des nombres de zéro à dix-neuf. Un nombre constitué d'un seul chiffre constitue le point terminal de la récursivité, et on renvoie tout simplement son équivalent en français.

Si le nombre reçu est compris dans les intervalles 10..99 , alors on considère que l'évaluation du nombre est égale au chiffre des dizaines plus l'évaluation (appel récursif) des unités. On distinguera ici les cas où on doit insérer un « ET » et les cas des dizaines « soixante-dix » et « quatre-vingt-dix ».

Si le nombre reçu est compris dans les intervalles 70..79 ou 90..99 alors l'évaluation est égale au chiffre des dizaines (lu dans le tableau) décrémenté de un plus l'évaluation (appel récursif) du chiffre des unités incrémenté de 10. On distinguera ici les cas où on doit insérer un « ET » .

Si le nombre reçu est compris dans l'intervalle 100..999 alors l'évaluation est égale au chiffre des centaines (exception faite du nombre 100) plus la chaîne « cent » plus une évaluation (appel récursif) du reste. On prendra en compte le cas du « s » final qui vient s'ajouter au « cent » dans certains cas.

Si le nombre est supérieur à 999 alors on détecte d'abord sa puissance de mille (mille, million, milliard…) qui constitue ce qu'on a appelé ci-dessus la partie principale, on l'évalue par un appel récursif (en lui collant ensuite la puissance de mille correspondante) et on lui concatène le reste qui est évalué par un appel récursif.

Voici un exemple des appels récursifs pour le nombre donné plus haut.

Code des exemples : chap_IV_13.zip Miroir 1 , chap_IV_13.zip Miroir 2