III. Les échecs▲
III-A. Le parcours du fou▲
Nous avons un échiquier et un fou situé dans un coin noir. Il faut faire arriver ce dernier dans le coin opposé, en le faisant passer une seule fois sur une case, dans le même sens de déplacement. Cela signifie que le fou ne peut pas passer deux fois par la même case en ayant le même sens de déplacement.
exemple : un fou a deux sens de déplacement. On décide que le premier sens, nommé A, et le deuxième sens, nommé B, sont indiqués sur les dessins suivants :
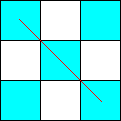
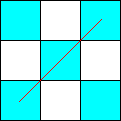
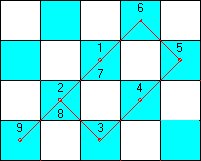
Ainsi, le parcours correspondant à l'image ci-dessous n'est pas possible, car le fou parcourt les cases 1,2,3,4,5,6 sans problème, mais ensuite il va de 7 (numéroté aussi 1) en 8 (numéroté aussi 2) dans le sens B (défini ci-dessus). Or, la case 1 avait déjà été visitée dans le sens B, pour aller dans la case 2. De même, le fou ne peut aller de la case 9 à la case 6 en passant par les cases 2 et 1, car ces deux cases ont déjà été visitées dans le sens B.
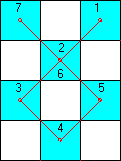
En revanche, le parcours correspondant au dessin suivant est possible, car le fou parcourt les cases 1,2,3 dans le sens B. Ensuite, une fois arrivé en 5 il passe à nouveau dans la case 2 (numérotée aussi 6), mais cette fois-ci dans le sens A. Une fois en 6, il ne pourra aller qu'en 7 car les cases 1 et 3 ont déjà été parcourues dans le sens B, et la case 5 a déjà été parcourue dans le sens A quand on est allé de 5 vers 6.
Nous allons créer l'algorithme de ce programme. On a un échiquier dont chaque case est associée à deux sens. Pour savoir si toutes les cases ont été parcourues, on ne peut pas compter le nombre de sauts, car on ne sait pas combien il y en a. En effet, le fou peut passer 2 fois sur une même case, et ceci pour n cases. Nous devons donc associer aussi aux cases une valeur booléenne, dont le rôle sera d'indiquer qu'elle a été visitée ou non. Si toutes les cases noires ont été visitées, alors on obtient un total de 32. Pendant le parcours, on doit mémoriser les numéros des cases parcourues, et, comme une case peut être visitée au maximum 2 fois, on a prévu un tableau de mémorisation dont la taille est égale au double du nombre de cases noires. Il est vrai que le fou ne peut aller dans les coins qu'une fois, donc il faudrait enlever 2 au résultat, mais le fait d'ajouter 2 éléments au tableau n'est pas un lourd handicap.
exemple : pour un échiquier de 8*8 cases, il y a (8*8)/2 = 32 cases noires. Le nombre de coups théorique est de 32*2 (passage 2 fois dans chaque case) moins 2 (les coins), soit 62.
Structures des données
const lim1 = 8;
lim2 = 8;
type case_ec = record
sensA,
sensB,
visite: boolean;
end;
echiquier = array[1..lim1, 1..lim2] of case_ec;
var ech: echiquier; //--- echiquier des coups joués
coups: array[1..lim1 * lim2] of integer; //--- liste des coups mémorisésOn écrit ensuite la fonction qui vérifie que toutes les cases ont été visitées:
function tout_a_ete_visite: boolean;
var i, j, total: integer;
begin
total := 0;
for i := 1 to lim1 do
for j := 1 to lim2 do
if ech[i, j].visite then inc(total);
tout_a_ete_visite := (total = (lim1 * lim2 div 2));
end;
La procédure qui simule le parcours du fou est bien entendu récursive. Elle a trois paramètres :
- x1 et y1 sont les coordonnées du fou au coup précédent
- coup : numéro du coup, utilisé pour mémoriser les déplacements du fou
Nous avons décidé d'arrêter l'algorithme après le premier parcours trouvé, mais rien ne vous empêche de supprimer le test sur la variable fini, pour laisser le programme chercher toutes les solutions.
Voyons le coeur du programme : on a quatre directions possibles, représentées par les tableaux dx et dy. A partir de chaque case, on essaye d'aller dans chacune des quatre directions, ce qui nous amène à l'utilisation d'une boucle for i:=1 to 4 do. On calcule ensuite les coordonnées de la prochaîne case, en utilisant les tableaux dx et dy : new_x:=x1+dx[i]; new_y:=y1+dy[i]; et on s'assure que cette case est bien sur l'échiquier. Suivant la valeur de i, on se trouve ou bien dans le sens A, ou bien dans le sens B. Supposons que nous sommes dans le sens A. Comme on va se déplacer dans une autre case, il faut sauvegarder les paramètres de la case en cours, marquer son sens A, marquer le sens A de la case où on va sauter (de cette façon, si on y repasse au bout de n sauts, on ne pourra pas utiliser le sens A), faire un appel récursif avec les coordonnées de la nouvelle case, et quand on sort de la récursion, restaurer les valeurs telles qu'elles étaient avant le saut. Il ne faut évidemment pas oublier de positionner à true le booléen visite de chaque case qui a été visitée au moins une fois.
Le même ensemble d'instructions s'applique pour le sens B; nous obtenons le programme suivant :
procedure chemin(x1, y1, coup: integer);
const dx: array[1..4] of integer = (1, 1, -1, -1); //--- 1 et 3 : sens 1
dy: array[1..4] of integer = (1, -1, -1, 1); //--- 2 et 4 : sens 2
var i, new_x, new_y: integer;
old_s11, old_s12, old_s21, old_s22, visit: boolean;
begin
coups[coup] := y1 * 10 + x1;
if tout_a_ete_visite then
begin
max_coups := coup;
fini := true;
end
else
begin
for i := 1 to 4 do
begin
new_x := x1 + dx[i];
new_y := y1 + dy[i];
if not fini then
if (new_x >= 1) and (new_x <= lim1) and
(new_y >= 1) and (new_y <= lim2) then
if (i mod 2) = 1 then
begin
if not ech[new_x, new_y].sensA then
begin
//--- sauvegarde anciennes valeurs
old_s11 := ech[new_x, new_y].sensA;
old_s12 := ech[x1, y1].sensA; //--- sauvegarde sensA
visit := ech[new_x, new_y].visite;
//--- modifications
ech[new_x, new_y].sensA := true;
ech[new_x, new_y].visite := true;
ech[x1, y1].sensA := true; //--- modif sensA
//--- appel récursif
chemin(new_x, new_y, coup + 1);
//--- restauration anciennes valeurs
ech[x1, y1].sensA := old_s12; //--- restaure sensA
ech[new_x, new_y].sensA := old_s11;
ech[new_x, new_y].visite := visit;
end;
end
else
begin
if not ech[new_x, new_y].sensB then
begin
//--- sauvegarde anciennes valeurs
old_s21 := ech[new_x, new_y].sensB;
old_s22 := ech[x1, y1].sensB;
visit := ech[new_x, new_y].visite;
//--- modifications
ech[new_x, new_y].sensB := true;
ech[new_x, new_y].visite := true;
ech[x1, y1].sensB := true;
//--- appel récursif
chemin(new_x, new_y, coup + 1);
//--- restauration anciennes valeurs
ech[x1, y1].sensB := old_s22;
ech[new_x, new_y].sensB := old_s21;
ech[new_x, new_y].visite := visit;
end;
end;
end;
end;
end;Code des exemples : chap_III_1.zip Miroir 1 , chap_III_1.zip Miroir 2
III-B. Le problème du cavalier▲
Un autre problème bien connu est le parcours du cavalier : comment faut-il faire jouer un cavalier sur un echiquier de façon à ce qu'il passe par toutes les cases de l'échiquier ?
- les parcours constituant un cycle fermé (c'est à dire que le cavalier, après avoir parcouru toutes les cases de l'échiquier se retrouve à la même position qu'au départ)
- les parcours constituant un cycle ouvert (le cavalier part d'une case quelconque et après avoir parcouru les 63 cases restantes il se retrouve sur une autre position que celle de départ.
Le problème du cavalier, par rapport à celui du fou ou des reines, est qu'il demande un temps considérable pour être résolu, cela à cause du grand nombre de combinaisons possibles.
Nous allons voir deux manières de résoudre ce problème.
Première solution
On considère l'échiquier comme un tableau en deux dimensions, représenté par la variable suivante : t : array[1..8,1..8] of byte.
Pour représenter les 8 directions, on s'aide de deux tableaux "t_x" et "t_y".
Quand le cavalier a sauté sur une case, alors la case est initialisée à 1, sinon à 0.
Un cavalier peut sauter dans 8 directions, mais le saut n'est pas toujours possible, notamment si le cavalier se trouve sur les bords de l'échiquier.
Pour chaque position du cavalier, on essaie les 8 directions; pour chaque direction possible, on met la case à 1 (simulation du saut), on sauvegarde la position dans un tableau et on fait un appel récursif; ensuite, une fois revenu, il faut annuler le coup, donc on remet la case à 0.
Voici le programme :
const t_x: array[1..8] of integer = (1, 2, 2, 1, -1, -2, -2, -1);
t_y: array[1..8] of integer = (-2, -1, 1, 2, 2, 1, -1, -2);
var t: array[1..8, 1..8] of byte; //--- l'échiquier
p: array[1..65] of integer; //--- mémorise les sauts consécutifs
s: string; //--- variable auxiliaire d'affichage
procedure remplir;
begin
fillchar(t, sizeof(t), 0);
end;
function on_peut_jouer(y, x, nr: byte): boolean;
begin
on_peut_jouer := false;
inc(x, t_x[nr]); inc(y, t_y[nr]);
if (x in [1..8]) and (y in [1..8]) then //--- si le cavalier est dans l'échiquier
on_peut_jouer := t[y, x] = 0; //--- et si la case n'est pas occupée
end;
procedure récursive(y, x, cpt: byte);
var a: byte;
begin
if cpt = 64 then
begin
s := '';
for a := 1 to 64 do s := s + inttostr(p[a]) + ';';
inc(nb);
form1.edit1.text := 'solution numéro : ' + inttostr(nb) + ' : ' + s;
end
else
for a := 1 to 8 do
if on_peut_jouer(y, x, a) then
begin
t[y + t_y[a], x + t_x[a]] := 1;
p[cpt] := x * 10 + y;
récursive(y + t_y[a], x + t_x[a], cpt + 1);
form1.edit2.text := inttostr(y + t_y[a]);
t[y + t_y[a], x + t_x[a]] := 0;
end;
end;
procedure debut;
var ligne, colonne: byte;
begin
remplir;
ligne := 1;
colonne := 1;
t[ligne, colonne] := 1;
récursive(ligne, colonne, 1);
t[ligne, colonne] := 0;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
debut;
end;Le problème de cette solution est qu'elle est extrêmement lente : le cavalier ne parcourt que 250.000 cases par minute.
Deuxième solution
Voici maintenant une deuxième solution beaucoup plus efficace :
on ne considère plus le parcours de l'échiquier comme un ensemble de cases devant être initialisées à 1 quand le cheval est passé dessus (et remise à 0 quand le cheval revient d'une descente récursive) mais comme un ensemble de liens; on numérote les cases de 1 à 64. Ainsi quand le cavalier saute de la case 1 à la case 11, on initialise le lien "1->11" avec la valeur 1, ensuite on initialise tous les liens arrivant en 11 avec la valeur 1 (ce sont "5->11","17->11","21->11","26->11","28->11"); ainsi, quand l'ordinateur arrivera sur l'une de ces cases, il ne prendra aucun de ces chemins. Le fait de couper à chaque mouvement les sauts possibles pour une case donnée fait que le nombre de possibilités est réduit (malgré cela, il est encore très grand) et le programme trouve des solutions beaucoup plus rapidement. A titre indicatif, la première solution est trouvée en quatre minutes sur un K6-350, au bout de 17 millions de sauts du cavalier. Dans cette version du programme, le cavalier parcourt 4,4 millions de cases par minute. Le gain de temps est énorme. Nous avons laissé tourner le PC pendant deux jours (ensuite nous l'avons arrêté); il a exploré 12 milliards de coups et a trouvé environ 9000 solutions.
Voici une représentation de l'échiquier utilisé dans cette version:
01 02 03 04 05 06 07 08
09 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64Si on saute de 1 en 11 alors les liens "05->11, 17->11, 21->11,26->11, 28->11" sont coupés; il faut les mémoriser avant le saut, pour les restaurer après, pendant la remontée des niveaux récursifs
Les autres structures de données nécessaires sont le tableau "nb_sauts", qui indique le nombre de sauts possibles pour chaque case de l'échiquier :
nb_sauts: array[1..64] of integer =
(2, 3, 4, 4, 4, 4, 3, 2,
3, 4, 6, 6, 6, 6, 4, 3,
4, 6, 8, 8, 8, 8, 6, 4,
4, 6, 8, 8, 8, 8, 6, 4,
4, 6, 8, 8, 8, 8, 6, 4,
4, 6, 8, 8, 8, 8, 6, 4,
3, 4, 6, 6, 6, 6, 4, 3,
2, 3, 4, 4, 4, 4, 3, 2);
pos_saut: array[1..64] of integer = // pour savoir à quelle position on doit
(1, 3, 6, 10, 14, 18, 22, 25, // chercher la case suivante lors d'un
27, 30, 34, 40, 46, 52, 58, 62, // saut;
65, 69, 75, 83, 91, 99, 107, 113, // on recherche la case suivante dans le
117, 121, 127, 135, 143, 151, 159, 165, // tableau "liens"
169, 173, 179, 187, 195, 203, 211, 217,
221, 225, 231, 239, 247, 255, 263, 269,
273, 276, 280, 286, 292, 298, 304, 308,
311, 313, 316, 320, 324, 328, 332, 335);
liens: array[1..336] of integer =
(11, 18, //----- liens "1->11", "1->18"
12, 17, 19, //----- liens "2->12", "2->17", "2->19"
9, 13, 18, 20,
10, 14, 19, 21,
...On a un total de 336 sauts pour 64 cases, soit une moyenne de 5,25 sauts par case.
Et comme on a 64 cases à parcourir, alors le nombre total de possibilités est de 5,25 élevé à la puissance 64, soit 1,23*1046.
On utilise aussi des tableaux auxiliaires, comme "occupe" qui est un tableau de 336 booléens indiquant si un lien a déjà été visité ou pas. Pour chaque lien occupé (1->11) on occupe les liens allant vers 11. Mais une fois remonté, on les restaure; on a donc besoin de tableaux mémorisant les liens qu'on va occuper à chaque saut. Cette mémorisation s'effectue de la façon suivante :
por := 0;
for j := 1 to 336 do // on occupe les liens
if liens[j] = new_x then
begin
inc(por);
po[por] := j;
oc[por] := occupe[j];
occupe[j] := true;
end;et la restauration des liens après le remontée récursive s'effectue de la manière suivante :
for j := 1 to por do occupe[po[j]] := oc[j];
procedure TForm1.Button4Click(Sender: TObject);
var num_saut, posit: integer;
procedure remplir1;
begin
fillchar(occupe, sizeof(occupe), #0);
end;
procedure sauter(x, numero_saut: integer);
var po: array[1..8] of integer;
oc: array[1..8] of boolean;
i, ii, j, k, m, por, new_x, c: integer;
s1: string;
begin
inc(num_saut);
if numero_saut > 63 then
begin
memo1.lines.clear;
memo1.lines.add('saut=' + inttostr(num_saut));
memo1.lines.add(soluce);
memo1.refresh;
exit;
end;
for i := 1 to nb_sauts[x] do
if not occupe[pos_saut[x] + i - 1] then
begin
c := pos_saut[x] + i - 1;
occupe[c] := true; // si x=1, "occupe[1]:=true" indique : lien "1->11" occupé
new_x := liens[c]; // new_x:=11,18
//--------- on occupe les liens
por := 0;
for j := 1 to 336 do
if liens[j] = new_x then
begin
inc(por);
po[por] := j;
oc[por] := occupe[j];
occupe[j] := true;
end;
//--------- appel récursif
s1 := inttostr(new_x) + ';';
soluce := soluce + s1;
sauter(new_x, numero_saut + 1);
delete(soluce, length(soluce) - length(s1) + 1, length(s1));
//--------- restauration des liens occupées
for j := 1 to por do occupe[po[j]] := oc[j];
occupe[c] := false;
end;
end;
begin // chercher solution
remplir1;
soluce := ''; num_saut := 1;
occupe[2] := true; // on interdit le saut "1->18" car symétrie avec "1->11"
posit := 1;
sauter(posit, 1);
end;Code des exemples : chap_III_2.zip Miroir 1 , chap_III_2.zip Miroir 2
III-C. Le problème des huit reines▲
Un problème dont tout le monde a entendu parler et qui peut se résoudre facilement par l'ordinateur est le suivant: comment placer 8 reines sur un échiquier sans que chacune "mange" au moins une des 7 autres ?
Ce problème se résout par des essais successifs; on applique la récursivité. Nous allons présenter ici plusieurs solutions, à commencer d'abord par une solution itérative, que nous transformerons ensuite en une solution récursive.
Première solution, itérative :
On dispose de l'échiquier, qui est vide au début. On sauvegarde l'échiquier dans un tableau auxiliaire. On fait 8 boucles imbriquées qui représentent les 8 lignes; chaque boucle va de 0 à 7 ce qui représente une boucle de la première colonne à la huitième colonne. On utilise aussi une chaîne de caractères qui va représenter les positions des reines sur l'échiquier.
Pour chaque position définie par les coordonnées "ligne,colonne" : - on vérifie si la case est vide - si oui alors : -- on occupe toutes les cases de l'échiquier dans les cinq directions décrites ci-dessous à partir de la position actuelle -- on mémorise la colonne dans une chaîne de caractères, qui représente en réalité la position da la reine se trouvant sur la ligne en cours -- on sauvegarde l'échiquier car il sera modifié par les coups suivants -- on passe à la ligne suivante, à la première colonne -- si on est à la dernière ligne alors on affiche la chaîne - sinon : -- on essaye la colonne suivante - si on est à la huitième colonne on sort de la boucle et on restaure l'échiquier
Voici les cinq directions dont il s'agissait ci-dessus :
+--------+ X représente une reine.
¦ ¦
¦444X0000¦ Etant donné qu'on pose les 8 reines en descendant sur
¦ 321 ¦ l'échiquier, cela n'a pas de sens de compléter les 3
¦ 3 2 1 ¦ directions vers le haut, car on vient d'en haut et l'échiquier
¦3 2 1 ¦ a déjà été complété par un coup précédent.
+--------+const max = 8;
dx: array[0..4] of integer = (1, 1, 0, -1, -1);
dy: array[0..4] of integer = (0, 1, 1, 1, 0);
type tab = array[0..max - 1, 0..max - 1] of byte;
procedure occuper_toutes_les_directions(var tt: tab; xx, yy, valeur: byte);
var i, colonne, ligne: integer;
begin
tt[xx, yy] := valeur;
for i := 0 to 4 do
begin
colonne := xx; ligne := yy;
inc(colonne, dx[i]); inc(ligne, dy[i]);
while (ligne in [0..7]) and (colonne in [0..7]) do
begin
tt[ligne, colonne] := valeur;
inc(colonne, dx[i]); inc(ligne, dy[i]);
end;
end;
end;
procedure jouer;
var x0, x1, x2, x3, x4, x5, x6, x7: byte;
st: string[8];
tab_sauve: array[0..7] of tab;
begin
st := ' '; // pour mémoriser les positions
fillchar(t[0], sizeof(t), #0); // initialisation plateau
move(t, tab_sauve[0], 64);
form1.memo1.lines.clear;
for x0 := 0 to max - 1 do
if t[0, x0] = 0 then
begin
occuper_toutes_les_directions(t, x0, 0, 2);
st[1] := chr(48 + x0);
move(t, tab_sauve[1], 64);
for x1 := 0 to max - 1 do
if t[1, x1] = 0 then
begin
occuper_toutes_les_directions(t, x1, 1, 2);
st[2] := chr(48 + x1);
move(t, tab_sauve[2], 64);
for x2 := 0 to max - 1 do
if t[2, x2] = 0 then
begin
occuper_toutes_les_directions(t, x2, 2, 2);
st[3] := chr(48 + x2);
move(t, tab_sauve[3], 64);
for x3 := 0 to max - 1 do
if t[3, x3] = 0 then
begin
occuper_toutes_les_directions(t, x3, 3, 2);
st[4] := chr(48 + x3);
move(t, tab_sauve[4], 64);
for x4 := 0 to max - 1 do
if t[4, x4] = 0 then
begin
occuper_toutes_les_directions(t, x4, 4, 2);
st[5] := chr(48 + x4);
move(t, tab_sauve[5], 64);
for x5 := 0 to max - 1 do
if t[5, x5] = 0 then
begin
occuper_toutes_les_directions(t, x5, 5, 2);
st[6] := chr(48 + x5);
move(t, tab_sauve[6], 64);
for x6 := 0 to max - 1 do
if t[6, x6] = 0 then
begin
occuper_toutes_les_directions(t, x6, 6, 2);
st[7] := chr(48 + x6);
for x7 := 0 to max - 1 do
if t[7, x7] = 0 then
form1.memo1.lines.add(st + chr(48 + x7));
move(tab_sauve[6], t, 64);
end;
move(tab_sauve[5], t, 64);
end;
move(tab_sauve[4], t, 64);
end;
move(tab_sauve[3], t, 64);
end;
move(tab_sauve[2], t, 64);
end;
move(tab_sauve[1], t, 64);
end;
move(tab_sauve[0], t, 64);
end;
end;Deuxième solution, récursive :
Nous allons maintenant transformer toutes ces boucles imbriquées en une procédure récursive, comme on l'a déjà vu.
En tenant compte du fait que la récursivité a la propriété d'empiler les variables locales à une procédure, nous allons déclarer un échiquier local dans lequel on va faire les sauvegardes de l'échiquier, ainsi que la position du pion en cours, c'est à dire la chaîne "st".
Etant donné que la procédure comporte huit boucles, nous allons rajouter un paramètre à la procédure "jouer", qui représente le numéro de la ligne, et un autre paramètre pour la chaîne de caractères; en même temps il ne faut pas oublier que d'une procédure à l'autre (en réalité d'un niveau "n" pendant la récursivité, au niveau "n+1") on doit transmettre l'échiquier.
procedure jouer1(ligne: integer; var t: tab; st: string); // récursive 1
var colonne: byte;
tab_sauve: tab;
begin
move(t, tab_sauve, 64);
for colonne := 0 to max - 1 do
if t[ligne, colonne] = 0 then
begin
occuper_toutes_les_directions(t, colonne, ligne, 2);
if ligne < 7 then
jouer1(ligne + 1, st + chr(49 + colonne))
else
form1.memo1.lines.add(st + chr(49 + colonne));
move(tab_sauve, t, 64);
end;
end;Troisième solution, récursive :
Nous allons voir maintenant comment on peut améliorer ce programme du point de vue de la rapidité; pour commencer, nous n'allons plus remplir l'échiquier dans les 5 directions à chaque coup, mais nous allons vérifier si une case se trouve dans la ligne de mire d'une reine précédente; pour cela on fait une fonction "occupé", qui ne vérifie que les trois directions manquantes, celles qui vont vers le haut.
const max = 8;
dx2: array[0..2] of integer = (-1, 0, 1);
dy2: array[0..2] of integer = (-1, -1, -1);
function occupe2(x, y: integer; t: tab): boolean;
var i, colonne, ligne: integer;
sortir: boolean;
begin
i := -1; sortir := false;
repeat
inc(i); colonne := x; ligne := y;
dec(colonne, dx2[i]); dec(ligne, dy2[i]);
repeat
inc(colonne, dx2[i]); inc(ligne, dy2[i]);
if (colonne in [0..max - 1]) and (ligne >= 0) then
sortir := (t[ligne, colonne] <> 0);
until (colonne = -1) or (colonne = max) or (ligne = -1) or sortir;
until (i = 2) or sortir; // i=0,1,2 : les trois directions
occupe2 := sortir;
end;
procedure jouer2(ligne: byte; var t: tab; st: string);
var x: byte;
begin
for x := 0 to max - 1 do
if not occupe2(x, ligne) then
begin
t[ligne, x] := 1; // on pose une reine
if ligne < max - 1 then
jouer(ligne + 1, t, st + chr(49 + x))
else
form1.memo1.lines.add(st + chr(49 + x));
t[ligne, x] := 0; // on enlève la reine
end;
end;Quatrième solution, récursive :
Il y a d'autres solutions à ce problème. Par exemple, l'échiquier est représenté par une chaîne de 8 caractères. Chacun des 8 caractères représente une ligne de l'échiquier, et la colonne est représentée par le numéro inscrit dans la chaîne.
Supposons qu'on a la situation suivante :
- une reine en ligne 1, colonne 1
- une reine en ligne 2, colonne 3
- une reine en ligne 3, colonne 5
La chaîne est donc égale à : st='13500000'.
Supposons qu'on veuille placer une reine sur la quatrième ligne; pour cela il faut que la quatrième ligne de l'échiquier soit vide, c'est à dire qu'il faut que le quatrième élément de la chaîne soit '0'.
Ensuite il faut parcourir les huit colonnes de cette ligne et dès qu'il y a une case qui ne soit pas en danger, y placer une reine. Pour savoir si la case n'est pas en danger il faut vérifier si la colonne n'a pas déjà été occupée.
Ainsi si on veut placer une reine en quatrième ligne et première colonne, on ne peut pas car la première colonne (notée par "1" dans la chaîne "st" ) a déjà été utilisée par la première reine.
Par contre la deuxième colonne n'a pas encore été utilisée, car la chaîne "st" ne contient pas le chiffre "2"; pour savoir si on peut placer une reine, il ne nous reste plus qu'à vérifier les diagonales en partant de la position actuelle qui est ligne 4, colonne 2; il ne faut pas qu'on ait une reine sur les positions suivantes:
ligne 3, colonne 1 ---> première diagonale, gauche,haut
ligne 3, colonne 3 +
ligne 2, colonne 4 ¦--> deuxième diagonale, droite, haut
ligne 1, colonne 5 +On remarque que pour faire les tests sur la diagonale on décrémente de 1 la ligne et on décrémente (ou incrémente) de 1 la colonne, et ceci jusqu'à sortir de l'échiquier (en fait arriver aux bords de "st") ou rencontrer une reine. La fonction qui vérifie les diagonales s'appelle "test" et elle est récursive. La procédure qui place les reines sur l'échiquier est elle aussi récursive. On a le programme :
function test(ligne, colonne, delta: integer; var st: string): boolean;
begin
if (ligne in [0, max + 1]) or (colonne in [0, max + 1]) then
test := true
else
test := (st[ligne] <> chr(48 + colonne)) and test(ligne - 1, colonne + delta, delta, st)
end;
procedure jouer3(lg: integer; st: string);
var col: integer;
begin
if lg = max + 1 then
form1.memo1.lines.add(st)
else
for col := 1 to max do
if (pos(chr(col + 48), st) = 0) and test(lg, col, -1, st) and test(lg, col, 1, st) then
begin
st[lg] := chr(48 + col);
jouer3(lg + 1, st);
st[lg] := '0';
end;
end;Et voici les appels à chacune de ces quatre procédures :
procedure TForm1.Button1Click(Sender: TObject);
var t: tab;
begin // cherche solution
memo1.Clear;
//---- solution itérative à 8 boucles
// jouer;
//---- solution récursive 1
//fillchar(t,sizeof(t),#0);
//jouer1(0,t,'');
//---- solution récursive 2
//fillchar(t,sizeof(t),#0);
//jouer2(0,t,'');
//---- solution récursive 3
jouer3(1, ' '); // chaîne de 8 espaces
end;Code des exemples : chap_III_3.zip Miroir 1 , chap_III_3.zip Miroir 2


