VII. Les arbres▲
VII-A. Les arbres binaires▲
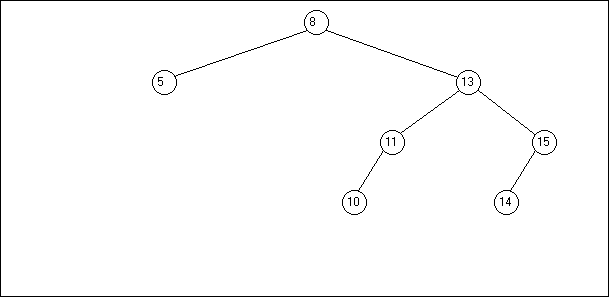
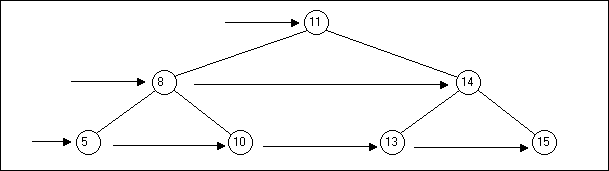
Un arbre binaire est un graphe (un ensemble de sommets) connexe (il n'y a pas de sommet isolé) sans cycle (il n'y a pas de boucle) dont la représentation graphique est la suivante :
L'arbre est dit binaire car chaque noeud possède au plus deux fils : un fils gauche et un fils droit.
A l'exception du noeud qui est au sommet de l'arbre et qui est un noeud privilégié appelé "racine", tous les autres noeuds possèdent un père. Un noeud qui n'a pas de fils est appelé une feuille.
Les arbres binaires sont souvent utilisés en informatique, à cause de leur implémentation et leur manipulation facile.
Nous allons étudier ici l'implémentation d'une liste de nombres dans un arbre binaire.
Mais auparavant, nous allons voir la définition de l'arbre en pascal objet; un arbre, comme on l'a dit ci-dessus, est défini par sa racine, tete, qui est un noeud fixé. Comme on doit parfois se déplacer dans l'arbre sans utiliser obligatoirement une procédure récursive (en raison de sa structure qui s'y prête fortement), on a aussi une variable auxiliaire (nommée courant, de type noeud).
Chaque noeud est défini par un entier, et deux fils (noeuds), sans oublier les procédures de création et de destruction du noeud :
noeud = class
private
entier: integer;
gauche, droite: noeud;
constructor create(nb: integer);
destructor destroy;
end;L'arbre est défini par les deux variables tete et courant, sans oublier les deux procédures de construction et de destruction :
arbre = class
private
tete, courant: noeud;
public
constructor create(nb: integer);
destructor destroy;
end;- le parcours et l'affichage
- l'ajout d'un noeud dans l'arbre
- le compte du nombre de noeuds d'un arbre
- le compte du nombre de niveaux
- l'équilibrage d'un arbre
- la comparaison de deux arbres
VII-A-1. Affichage d'un arbre▲
On peut parcourir un arbre pour faire des opérations sur ses noeuds, comme des modifications, des ajouts ou tout simplement des affichages.
Plusieurs parcours sont possibles pour afficher un arbre :
- les parcours en profondeur
- les parcours en largeur
Les parcours en profondeur
1) Le parcours (ou ordre) préfixé : on affiche le contenu du noeud dès qu'on est dessus, ensuite on parcourt son fils gauche puis son fils droit; le sens du parcours étant indiqué par des flèches liées au trajet (voir le parcours postfixé) :
La procédure permettant de faire un parcours préfixé est la suivante :
procedure aff(n: noeud);
begin
if n = nil then exit; // test de sortie de la procédure récursive
edit5.text := edit5.text + intToStr(n.entier) + ';'; // chaîne qui sera affichée
aff(n.gauche); // parcours fils gauche
aff(n.droite); // parcours fils droit
end;
Ainsi, un parcours préfixé pour cet arbre va nous donner comme résultat :
11;8;5;10;14;13;15
2) Le parcours (ou ordre) infixé : on affiche le contenu du noeud après avoir parcouru et affiché le contenu de son fils gauche; une fois que c'est fait, on parcourt et on affiche son fils droit :
La procédure permettant de faire un parcours infixé est la suivante :
procedure aff(n: noeud);
begin
if n = nil then exit; // test de sortie
aff(n.gauche); // parcours fils gauche
edit6.text := edit6.text + intToStr(n.entier) + ';'; // affichage noeud courant
aff(n.droite); // parcours fils droit
end;On l'appelle avec l'instruction suivante : aff(arbre_nb.tete);
Un parcours infixé pour cet arbre va nous donner comme résultat :
5;8;10;11;13;14;15
On constate que c'est aussi un tri par ordre croissant
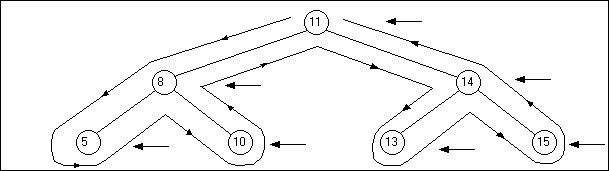
3) Le parcours (ou ordre) postfixé : on affiche le contenu du noeud après avoir parcouru et affiché ses deux fils :
La procédure permettant de faire un parcours postfixé est la suivante :
procedure aff(n: noeud);
begin
if n = nil then exit;
aff(n.gauche);
aff(n.droite);
edit7.text := edit7.text + intToStr(n.entier) + ';';
end;On appelle cette procédure comme les deux procédures précédentes : aff(arbre_nb.tete);
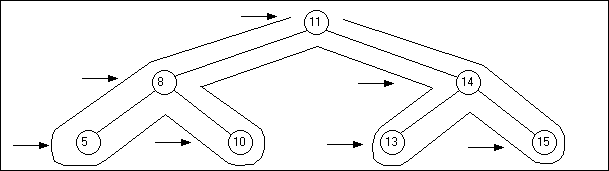
Le parcours en largeur
Le parcours en largeur est défini par le dessin suivant :
Le parcours en largeur n'est pas souvent utilisé dans la manipulation des arbres. Néanmoins, nous allons expliquer la manière dont on le réalise. Le temps requis pour faire ce parcours n'est plus linéaire. Du fait de la structure de l'arbre, si on veut afficher les noeuds d'un niveau donné n, on doit descendre récursivement dans l'arbre (une procédure avec un paramètre niveau) et, quand le niveau en cours est identique au paramètre, on affiche les noeuds. On quitte ensuite la procédure. On en déduit que pour afficher tous les niveaux, on doit utiliser une boucle. Voici la procédure correspondante :
procedure TForm1.Button13Click(Sender: TObject);
var i, j: integer;
procedure aff(n: noeud; niveau_courant, niveau: integer);
begin
if n = nil then exit;
if niveau = niveau_courant then
edit9.text := edit9.text + intToStr(n.entier) + ';'
else
begin
aff(n.gauche, niveau_courant + 1, niveau);
aff(n.droite, niveau_courant + 1, niveau);
end;
end;
begin // affichage largeur
edit9.text := '';
if arbre_nb = nil then exit;
j := arbre_nb.compter_niveaux(arbre_nb.tete);
for i := 1 to j do
aff(arbre_nb.tete, 1, i);
end;VII-A-2. Ajout d'un noeud dans un arbre▲
L'ajout d'un nombre (en réalité d'un noeud, car un nombre est introduit dans un arbre sous la forme d'un noeud) dans un arbre se fait de la façon suivante : si le nombre est le premier de l'arbre, alors on fait tout simplement une création de noeud, représentant la tête de l'arbre. Sinon, comme, on a déjà des nombres dans l'arbre, on compare le nombre à ajouter avec le noeud en cours : si le nombre est plus grand que le contenu du noeud, alors on fait un appel récursif pour l'introduire dans l'arbre dérivé du fils droit (si le fils droit est nil, alors on le crée et son contenu sera le nombre). Mais, si le nombre est plus petit que le contenu du noeud, alors on fait un appel récursif pour l'introduire dans l'arbre dérivé du fils gauche (si le fils gauche est nil, alors on le crée et son contenu sera le nombre qu'on veut introduire).
procedure noeud.ajouter(nb: integer);
begin
if nb >= entier then
if droite <> nil then
droite.ajouter(nb)
else
droite := noeud.create(nb)
else
if gauche <> nil then
gauche.ajouter(nb)
else
gauche := noeud.create(nb);
end;VII-A-3. Comptage des noeuds d'un arbre▲
Pour compter les noeuds d'un arbre, on calcule, pour chaque noeud qui existe, une somme égale à un à laquelle on additionne la somme des noeuds du fils gauche et la somme des noeuds du fils droit. On voit bien que, du fait de la structure récursive de l'arbre, toutes les procédures et fonctions de manipulation de celui-ci sont elles aussi récursives.
function arbre.compter_noeuds(posit: noeud): integer;
begin
if posit = nil then compter_noeuds := 0
else
compter_noeuds := 1 + compter_noeuds(posit.gauche) + compter_noeuds(posit.droite);
end;VII-A-4. Comptage des niveaux d'un arbre▲
Pour compter les niveaux d'un arbre, on doit d'abord compter les niveaux du fils gauche, ensuite les niveaux du fils droit, comparer les deux et garder le plus grand, puis enfin ajouter 1, car il faut aussi prendre en compte le niveau du noeud sur lequel on se trouve. En effet, supposons qu'on a un arbre avec seulement la tête. Le fils droit est nil, donc il a 0 niveaux; idem pour le fils gauche. Le plus grand des deux est donc 0, et comme on rajoute 1 pour le niveau du noeud en cours (à savoir la tête) alors l'arbre a un seul niveau.
function arbre.compter_niveaux(posit: noeud): integer;
var ng, nd: integer;
begin
if posit = nil then compter_niveaux := 0
else
begin
ng := 1 + compter_niveaux(posit.gauche);
nd := 1 + compter_niveaux(posit.droite);
if ng > nd then compter_niveaux := ng else compter_niveaux := nd;
end;
end;VII-A-5. Equilibrage d'un arbre▲
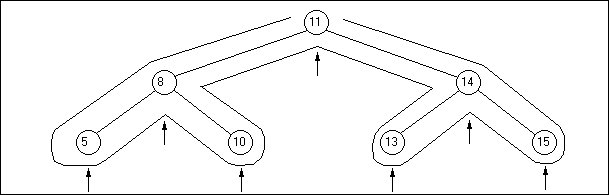
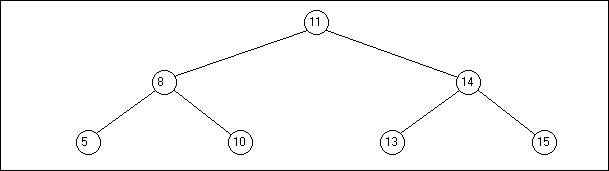
Un arbre de niveau n est dit équilibré si tous ses noeuds jusqu'au niveau n-1 existent, et si, dans le parcours linéaire du dernier niveau, il n'y a pas de noeud manquant. C'est ainsi que l'arbre du dessin a) n'est pas équilibré, alors que celui du b) l'est :
Même si le noeud contenant le nombre 15 n'avait pas existé, l'arbre aurait été équilibré, car il respecte bien la définition : tous les noeuds de niveau 2 existent, et, dans le parcours linéaire du dernier niveau, il n'y a pas de noeud manquant.
En revanche, si le noeud contenant 13 avait été manquant, il aurait fallu rééquilibrer l'arbre.
Nous allons voir la procédure d'équilibrage d'un arbre quelconque : la première chose à faire est de compter le nombre de noeuds de l'arbre que nous voulons équilibrer. Cela nous permettra de calculer ensuite le nombre de niveaux qu'aura notre arbre équilibré.
- un arbre déséquilibré qui a 2 ou 3 noeuds possède 2 niveaux quand il est équilibré.
- un arbre qui a de 4 à 7 noeuds possède 3 niveaux quand il est équilibré
- un arbre qui a de 8 à 15 noeuds possède 4 niveaux quand il est équilibré
Une fois que ce calcul est fait, il faut créer un arbre équilibré ayant n noeuds, tous initialisés à 0. Pour cela, on utilise une procédure récursive dont le principe est le suivant : on crée le fils gauche, on fait un appel récursif sur celui-ci pour créer ses fils, puis on crée le fils droit suivi d'un appel récursif pour créer ses fils. Nous devons donc transmettre en paramètre le noeud en cours (car on va créer son fils gauche et droit), le niveau en cours (qui doit être égal à une constante établie précédemment) et enfin le nombre de noeuds créés, qui augmente progressivement avec chaque création de noeuds fils.
procedure creer_arbre(n: noeud; niv: integer; var nb_n: integer);
begin
if nb_n = nb_noeuds then exit; // tous les noeuds nécessaires ont été créés
if niv < nb_niv then
begin
n.gauche := noeud.create(0);
inc(nb_n);
creer_arbre(n.gauche, niv + 1, nb_n);
n.droite := noeud.create(0);
inc(nb_n);
creer_arbre(n.droite, niv + 1, nb_n);
end;
end;Maintenant que cet arbre est créé, il faut le remplir avec les valeurs. Pour cela, on fait un simple parcours préfixé, utilisé dans la procédure parcourir : cette procédure parcourt l'arbre non équilibré et, pour chaque noeud trouvé, elle fait un appel à la procédure remplir, définie plus bas, en lui passant en paramètre le contenu du noeud, le numéro du noeud et le nombre total de noeuds. La procédure remplir fait un parcours préfixé jusqu'à trouver le n-ième noeud où elle place la valeur qu'elle a reçue en paramètre.
procedure parcourir(n: noeud; var nb: integer);
begin
if n = nil then exit;
parcourir(n.gauche, nb);
inc(nb); remplir(arbre_eq.tete, n.entier, nb, nb_noeuds);
parcourir(n.droite, nb);
end;
procedure remplir(n: noeud; valeur, posit, nb_n: integer);
var n1: integer;
begin
if nb_n = 1 then
n.entier := valeur
else
begin
n1 := 1;
while nb_n > n1 do n1 := n1 * 2;
if posit = (n1 div 2) then
n.entier := valeur
else
if posit < (n1 div 2) then
remplir(n.gauche, valeur, posit, arbre_nb.compter_noeuds(n.gauche))
else
remplir(n.droite, valeur, posit - (n1 div 2), arbre_nb.compter_noeuds(n.droite));
end;
end;VII-A-6. Comparaison de deux arbres▲
La comparaison de deux arbres se fait de la façon suivante : deux objets de type arbre sont égaux s'ils sont tous les deux égaux à nil, ou si leurs deux têtes sont égales. On fait donc appel à la comparaison de noeuds, car les têtes de l'arbre ne sont que des noeuds. Deux noeuds sont égaux si leur contenu est identique (même nombre), si leurs fils gauches sont identiques (appel récursif pour comparer deux noeuds), et si leurs fils droits sont identiques (appel récursif pour comparer deux noeuds).
function noeud.egal_a(noeud2: noeud): boolean;
begin
if (self = nil) and (noeud2 = nil) then
egal_a := true
else
if ((self <> nil) and (noeud2 = nil)) or
((self = nil) and (noeud2 <> nil)) or
(entier <> noeud2.entier) then
egal_a := false
else
egal_a := gauche.egal_a(noeud2.gauche) and droite.egal_a(noeud2.droite);
end;
function arbre.egal_a(arbre2: arbre): boolean;
begin
if (self = nil) and (arbre2 = nil) then egal_a := true
else
if (self = nil) and (arbre2 <> nil) then egal_a := false
else
if (self <> nil) and (arbre2 = nil) then egal_a := false
else
egal_a := tete.egal_a(arbre2.tete);
end;VII-A-7. Source de l'exemple▲
Code des exemples : chap_VII_1.zip Miroir 1 , chap_VII_1.zip Miroir 2
VII-B. Le code Morse▲
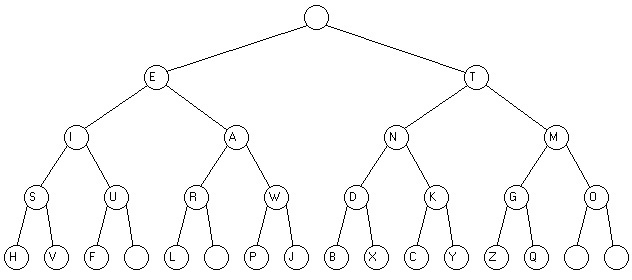
En utilisant les techniques des arbres binaires, on peut facilement réaliser un programme qui représente graphiquement le code Morse par un arbre binaire. Dans cet arbre on considère seulement les lettres de A à Z, car leur représentation tient sur 5 niveaux. On rappelle que le code Morse est constitué de points et de tirets : ainsi le "S" est représente par 3 points "..." et le "O" par trois tirets "---". On considère que les points sont représentés par un fils gauche d'un noeud, et un tiret par un fils droit d'un noeud. Voici la représentation graphique d'un arbre contenant l'alphabet:
Nous devons réaliser le programme qui dessine cet arbre. On utilise une chaîne de caractères pour stocker les lettres. Il faut savoir que l'alphabet Morse a plus de caractères que ce que nous avons choisi, qui font qu'un arbre binaire descend à sept niveaux. C'est pourquoi nous nous sommes limités seulement à 5 niveaux, et nous avons rempli les caractères manquants par des espaces.
Pour réaliser cet arbre, nous utilisons le parcours préfixe que nous avons vu précédemment et nous utilisons une formule mathématique afin d'introduire à chaque noeud de l'arbre le caractère correspondant.
La chaîne de caractères est donc, en fonction du parcours préfixe, la suivante :
const st : string = ' EISHVUF ARL WPJTNDBXKCYMGZQO ';
Les structures de données utilisées sont les suivantes :
noeud = class
private
carac: char;
gauche, droite: noeud;
constructor create(c: char);
destructor destroy;
procedure creer(nb, niv: integer);
procedure afficher(x, y, l: integer);
end;
arbre = class
private
tete, courant: noeud;
public
constructor create(c: char);
destructor destroy;
procedure afficher(x, y, l: integer);
end;
constructor noeud.create(c: char);
begin
carac := c;
gauche := nil; droite := nil;
end;
destructor noeud.destroy;
begin
if gauche <> nil then gauche.destroy;
if droite <> nil then droite.destroy;
end;
procedure noeud.afficher(x, y, l: integer);
begin
with form1.image1.picture.bitmap.canvas do
begin
ellipse(x, y, x + 25, y + 25);
textOut(x + 5, y + 5, carac);
if gauche <> nil then
begin
moveto(x + 3, y + 20); lineto(x - (l div 2) + 10, y + 70);
gauche.afficher(x - (l div 2), y + 60, l div 2);
end;
if droite <> nil then
begin
moveto(x + 22, y + 20); lineto(x + (l div 2) + 10, y + 70);
droite.afficher(x + (l div 2), y + 60, l div 2);
end;
end;
end;
procedure noeud.creer(nb, niv: integer);
var i: integer;
begin
if niv < 5 then
begin
gauche := noeud.create(st[nb + 1]);
gauche.creer(nb + 1, niv + 1);
i := nb + (round(exp((5 - niv) * ln(2))));
droite := noeud.create(st[i]);
droite.creer(i, niv + 1);
end;
end;
//--------------------------------------
constructor arbre.create(c: char);
begin
tete := noeud.create(c);
courant := tete;
end;
destructor arbre.destroy;
begin
courant := nil;
tete.destroy;
end;
procedure arbre.afficher(x, y, l: integer);
begin
tete.afficher(x, y, l);
end;
//--------------------------------------
procedure TForm1.FormCreate(Sender: TObject);
begin
morse := nil;
image1.picture.bitmap := tbitmap.create;
with image1.picture.bitmap do
begin
width := 639; height := 500;
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
morse := arbre.create(' ');
morse.tete.creer(1, 1);
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
morse.afficher(image1.width div 2 - 10, 10, image1.width div 2);
end;Nous allons expliquer maintenant la création de l'arbre.
Le sommet contient un espace.
A gauche du sommet on a la lettre "E" et à droite la lettre "T", c'est à dire les positions 2 et 17 de notre chaîne de caractères "st". 2=1+1 et 17=1+16.
Au niveau suivant, à gauche du "E" on a "I" et à droite "A", c'est à dire les positions 3 et 10 de notre chaîne de caractères "st". Mais 3=2+1 et 10=2+8, où 2 est la position de "E" dans "st".
Au niveau suivant, à gauche de "I" on a "S" et à droite "U", c'est à dire les positions 4 et 7 de notre chaîne de caractères "st". Mais 4=3+1 et 7=3+4.
On constate donc que le fils gauche d'un noeud à la valeur du père incrémenté de 1 (on parle des caractères qui sont dans la chaîne "st" : "E"+1="I"; "I"+1="S") et que le fils droit à la valeur du père incrémenté de 25-niveau. On lit cela "2 élevé à la puissance (5-niveau)". On rappelle qu'ici le sommet de l'arbre est au niveau 1, donc la lettre "E" est au niveau 2; par conséquent, le fils droit de "E" sera incrémenté de 8, car 23=8. De même, le fils droit du sommet sera incrémenté de 16, car 25-1 = 24 = 16.
Code des exemples : chap_VII_2.zip Miroir 1 , chap_VII_2.zip Miroir 2
VII-C. Évaluation d'une expression arithmétique▲
Nous convenons d'appeler "expression arithmétique" toute chaîne de caractères construite à partir de la liste des symboles 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, -, *, /, (, ).
Les expressions considérées ne mettront en jeu que des entiers relatifs.
Certaines expressions sont incorrectes comme "2+" (que nous pouvons toutefois interpréter comme "2+0" ) ou "3x(6+4". Nous supposerons dans ce qui suit que les expressions sont correctes.
Une expression arithmétique peut être représentée par un arbre binaire.
VII-C-1. La structure d'arbre binaire▲
L'arbre est dit binaire car chaque noeud "opérateur" possède deux fils : un fils gauche et un fils droit. Un noeud "opérateur" est un noeud qui contient un des symboles "+, -, * ou / ". Un noeud fils est soit un noeud opérateur, soit un noeud opérande - un entier - (c'est alors une feuille de l'arbre car il n'a pas de fils). La tête de l'arbre est toujours un noeud opérateur sauf dans le cas trivial où l'expression est réduite à un entier.
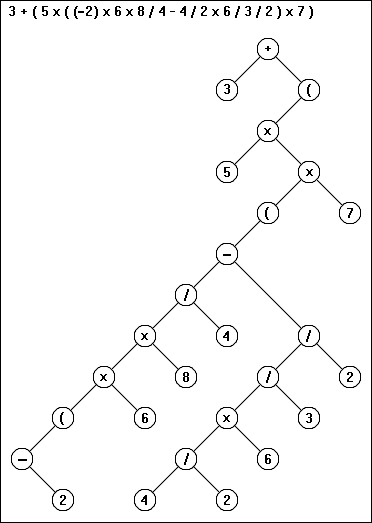
exemple : 3+(5*((-2)*6*8/4-4/2*6/3/2)*7)
Voici le dessin de l'arbre binaire correspondant à cette expression :
On constate que pour le nombre " - 2 ", tout en bas de l'arbre, à gauche, on n'a pas de fils droit. Dans ce cas on dit que le signe "-" (ce signe "-" bien précis) est un opérateur unaire, puisqu'il n'a qu'un fils. Cette notion d'opérateur unaire est applicable aussi pour les parenthèses, parce qu'elles n'ont qu'un fils au lieu de deux, comme devrait avoir tout noeud d'un arbre binaire. Il faut noter que par rapport au signe "-", la parenthèse ouvrante peut aussi bien avoir un fils gauche avec son contenu, qu'un fils droit. Ici, dans ce dessin, nous avons choisi délibérément le fils gauche, pour la distinguer du signe "-", qui, lui, a obligatoirement le fils à droite.
Ensuite, pour construire l'arbre, il faut faire attention au sens de lecture de l'expression.
ex. 3 : 8-4-4
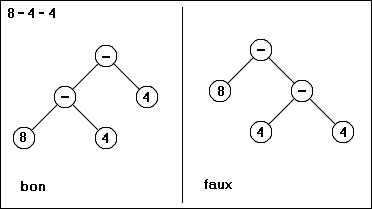
On voit dans cet exemple que l'expression doit être lue de droite à gauche. Lue de gauche à droite, l'expression conduirait à l'arbre de droite dont le résultat est manifestement faux car égal à 8.
Voici la déclaration sous Delphi (pascal objet) de la structure utilisée :
Noeud = class
private
op: char; //le genre du noeud : +, -, *, /, ou "c" s'il s'agit d'une feuille
valeur: integer; //dans le cas d'une feuille, sa valeur entière
FilsGauche, FilsDroit: Noeud;
public
constructor create;
destructor destroy;
end; { Noeud }
Arbre = class
private
tete, courant: noeud;
public
constructor create;
destructor destroy; override;
procedure Remplit(s: string);
function evalue(n: noeud): integer;
end; {arbre}Vous noterez que la procédure suivante, permettant de détruire un noeud, est récursive :
destructor noeud.destroy;
begin
if FilsGauche <> nil then FilsGauche.destroy;
if FilsDroit <> nil then FilsDroit.destroy;
inherited destroy;
end;En effet, FilsGauche.Destroy provoque un appel à noeud.destroy puisque FilsGauche est un noeud ! D'où le test "if FilsGauche<>nil...".
VII-C-2. Comment évaluer un arbre binaire▲
Pour évaluer le résultat d'un arbre, on applique tout simplement la formule suivante :
- si le noeud à évaluer contient un entier, le résultat est égal à cet entier.
- sinon, le résultat est égal à :
"evalue(FilsGauche) opération evalue(FilsDroit) ", où "opération" désigne l'un des quatre opérateurs usuels.
La procédure permettant d'évaluer le résultat de l'expression est la procédure récursive suivante :
function arbre.evalue(n: noeud): integer; //récursive, évidemment
begin
if n.op = 'c' then // c'est une feuille "chiffre"
evalue := n.valeur
else
begin // noeud opérateur
case n.op of
'+': evalue := evalue(n.FilsGauche) + evalue(n.FilsDroit);
'-': evalue := evalue(n.FilsGauche) - evalue(n.FilsDroit);
'*': evalue := evalue(n.FilsGauche) * evalue(n.FilsDroit);
'/': evalue := evalue(n.FilsGauche) div evalue(n.FilsDroit);
end;
end;
end;Un exemple d'appel de cette procédure est : UnArbre.Evalue(UnArbre.tete).
VII-C-3. Comment construire l'arbre binaire▲
Le travail le plus délicat ici n'est pas l'évaluation de l'arbre, mais la façon de le remplir à partir de la chaîne de caractères qui représente l'expression à évaluer.
C'est ce qu'on appelle la construction d'un arbre d'analyse par descente récursive.
Traitons pour commencer le cas où l'expression considérée ne comporte que des additions et des soustractions (et aucune parenthèse).
L'appel initial de la procédure "Remplit" reçoit l'expression entière comme paramètre.
Le principe de la procédure est que eval(a±b±c)=eval(a±b) ± c.
Pour cette expression, « a±b » est appelé "gauche" et "c" est appelé "droite". Nous nous ramenons toujours ainsi à l'évaluation de deux sous-expressions dont l'une est triviale (celle de droite, qui constitue une feuille de l'arbre).
Nous commençons par initialiser gauche à vide car gauche ne sera pas nécessairement affecté par la première partie de la procédure : en effet si on veut construire l'arbre de "-2" la partie gauche n'est pas initialisée.
Ensuite nous cherchons le premier signe "+" ou "-" en lisant l'expression de droite à gauche. Si nous n'en trouvons pas, c'est que l'expression est réduite à un entier et nous avons fini (condition de sortie de la récursion).
Sinon, nous coupons l'expression en deux (gauche et droite, de part et d'autre de l'opérateur trouvé), nous affectons au noeud courant le symbole opérateur trouvé et nous affectons à "droite" la valeur de l'entier isolé à droite, ce qui nous permet de remplir le fils droit du noeud opérateur de l'arbre dont nous étions partis.
Nous créons ensuite le fils gauche à partir de "gauche".
S'il est réduit à un entier, c'est fini (condition de sortie de la récursion).
S'il contient encore au moins un opérateur, il nous suffit de rappeler récursivement la procédure Remplit en lui passant "gauche" comme paramètre. Nous prenons au préalable la précaution de fixer le noeud courant au fils gauche actuel pour que le remplissage de l'arbre se poursuive au bon endroit.
Vous noterez que cette méthode permet d'évaluer certaines expressions "irrégulières" comme : +2+3, vide, 89, 5+97-, 78++5 ou "+".
C'est pour cette raison que nous introduirons la notion d'automate, après la procédure de création de l'arbre binaire, pour vérifier si une expression mathématique est correcte d'un point de vue syntaxique.
Mais voici d'abord une première version de la création d'un arbre :
procedure arbre.Remplit(s: string); //récursive !!!
var p, pp, pm: integer;
gauche, droite: string;
begin
//pour une expression du type a ± b ± c
gauche := '';
p := length(s);
while (p > 0) and (s[p] <> '+') and (s[p] <> '-') do dec(p);
if p > 0 then //il y a bien un "+" ou un "-" donc on a un arbre binaire
begin
gauche := copy(s, 1, p - 1);
droite := copy(s, p + 1, length(s));
courant.op := s[p]; //la tête, lors du premier appel
courant.FilsDroit := noeud.create;
courant.FilsDroit.op := 'c'; // c pour "chiffre"
if droite <> '' then
courant.FilsDroit.valeur := StrToInt(droite)
else
courant.FilsDroit.valeur := 0;
end
else //il n'y a pas/plus de "+" ni de "-", donc il reste un entier
begin
courant.op := 'c'; // c pour "chiffre"
if s <> '' then
courant.valeur := StrToInt(s)
else
courant.valeur := 0;
exit;
end;
//créons le fils gauche
courant.FilsGauche := noeud.create;
if gauche <> '' then
begin
p := length(s);
while (p > 0) and (s[p] <> '+') and (s[p] <> '-') do dec(p);
if p > 0 then
begin
courant := courant.FilsGauche;
Remplit(gauche); //il faut continuer --->>> APPEL RÉCURSIF
end
else //c'est fini
begin
courant.FilsGauche.op := 'c'; // c pour "chiffre"
courant.FilsGauche.valeur := StrToInt(gauche);
exit;
end;
end
else //on met un zéro
begin
courant.FilsGauche.op := 'c'; // c pour "chiffre"
courant.FilsGauche.valeur := 0;
end;
end;Nous allons maintenant modifier progressivement cette procédure pour arriver à la création d'un arbre binaire d'une expression contenant des parenthèses.
Tout d'abord nous allons créer une fonction "nb_elems" qui va recevoir comme paramètre une expression saisie au clavier, et qui va nous dire si cette expression contient un ou plusieurs éléments; si elle contient plusieurs éléments alors on va renvoyer comme réponse le nombre 2; on utilise cette valeur car un arbre binaire a deux fils au maximum; ainsi, comme nous l'avons vu précédemment, pour l'expression "2+3 - 5" on a l'arbre constitué des branches "2+3" et "5".
Cette fonction renvoie aussi la partie gauche et la partie droite d'une expression, d'où l'utilisation du mot "var g,d : string" dans les paramètres de la fonction.
Et elle renvoie aussi le signe qui est au sommet de l'arbre binaire (dans le cas des branches "2+3" et "5", le signe du sommet sera " - " ).
Nous devons transmettre aussi les séparateurs : " + " et " - " ensemble, ou bien " * " et " / " ensemble, car ce sont eux qui vont nous aider à délimiter la partie gauche de la partie droite.
Sachant que par la suite nous allons avoir des parenthèses, nous allons les prendre en compte dès maintenant en utilisant un compteur "nb" qui sera incrémenté chaque fois qu'on rencontrera une fermante (ne pas oublier que le sens de la lecture se fait de la droite vers la gauche, donc la première parenthèse susceptible d'être rencontrée sera fermante) et décrémenté chaque fois qu'on rencontrera une ouvrante.
function nb_elems(s: string; var g, d: string; s1, s2: char; var sig: char): integer;
var trouve: boolean;
p, nb: integer;
begin // on extrait la partie gauche et droite, séparées par s1 ou s2
p := length(s) + 1; nb := 0; // en faisant attention aux parenthèses, s'il y en a
repeat
dec(p);
if s[p] = '(' then dec(nb);
if s[p] = ')' then inc(nb);
trouve := (nb = 0) and ((s[p] = s1) or (s[p] = s2));
until (p = 1) or (trouve);
if p > 1 then // deux ou plusieurs elements; mais dans un arbre binaire il y en a 2
begin
d := copy(s, p + 1, length(s));
g := copy(s, 1, p - 1);
sig := s[p];
nb_elems := 2;
end
else // un seul élément
begin
d := s;
g := '';
sig := #0;
nb_elems := 1;
end;
end;Notre procédure initiale devient donc la procédure "traiter_sans_parentheses" qui va recevoir comme paramètres un noeud, l'expression saisie et les deux signes séparateurs (" +, - " ou bien " *, / ").
Supposons que notre expression contient une expression avec les quatre signes; au début les séparateurs sont les signes " + " et " - ".
Nous allons distinguer les deux cas, celui où on a deux éléments et celui où on n'en a qu'un :
- si on a deux fils, alors :
--- on crée le fils droit, on fait un appel récursif avec la nouvelle expression constitué de la partie droite et les deux nouveaux séparateurs " * " et " / ".
--- on met le signe qui séparait la partie droite de la gauche dans le nœud
--- on crée le fils gauche et on fait un appel récursif avec la nouvelle expression constituée de la partie gauche
- si on a un seul fils, alors :
--- ou bien les séparateurs initiaux étaient "+" et " - ", auquel cas on fait un appel récursif avec les séparateurs "*" et "/".
--- ou bien c'est un entier seul et on le met dans le noeud.
Voici donc cette procédure programmée, qu'on peut appeler avec l'instruction suivante :
"traiter_sans_parentheses(noeud1,expression,'+','-',gauche,droite,signe)"
procedure traiter_sans_parentheses(courant: noeud; s: string; signe1, signe2: char);
var g2, d2: string;
sig2: char;
begin
if nb_elems(s, g2, d2, signe1, signe2, sig2) = 2 then // deux termes ou plus
begin
courant.FilsDroit := noeud.create;
traiter_sans_parentheses(courant.FilsDroit, d2, '*', '/');
courant.op := sig2;
courant.FilsGauche := noeud.create;
traiter_sans_parentheses(courant.FilsDroit, g2, signe1, signe2);
end
else
if nb_elems(s, g2, d2, '*', '/', sig2) = 2 then
traiter_sans_parentheses(courant, s, '*', '/')
else
begin
courant.op := 'c'; // c pour "chiffre"
courant.valeur := strToInt(s);
end;
end;Les deux procédures ci-dessus vont se trouver dans notre nouvelle procédure "remplit", qui va traiter une expression contenant des parenthèses. Vous remarquerez que le corps de cette procédure est presque identique à celui de la procédure "traiter_sans_parentheses"; en effet on doit distinguer et traiter les deux cas possibles : un terme ou deux termes.
Si on a deux termes (par rapport aux signes en cours "+ -" ou " x / ", alors on les sépare et on fait un appel récursif.
Si on n'a qu'un seul terme, on doit distinguer les trois cas suivants :
- ou bien on a un seul terme par rapport à "+ -", auquel cas on fait un appel récursif avec " x / ".
- ou bien on a une seule parenthèse, auquel cas on fait un appel récursif avec l'intérieur de la parenthèse
--- ou bien on a un seul nombre
procedure arbre.Remplit(courant: noeud; s: string; signe1, signe2: char);
var g1, d1: string;
sig1: char;
function nb_elems(s: string; var g, d: string; s1, s2: char;
var sig: char): integer;
begin.... end;
procedure traiter_sans_parentheses(courant: noeud; s: string;
signe1, signe2: char);
begin.... end;
begin
if nb_elems(s, g1, d1, signe1, signe2, sig1) = 2 then // deux termes ou plus
begin
courant.FilsDroit := noeud.create;
remplit(courant.FilsDroit, d1, '*', '/');
courant.op := sig1;
courant.FilsGauche := noeud.create;
remplit(courant.FilsGauche, g1, signe1, signe2);
end
else // un seul terme
if nb_elems(s, g1, d1, '*', '/', sig1) = 2 then // un terme pour l'addition mais
remplit(courant, s, '*', '/') // plusieurs pour la multiplication : 2*3*(-5)
else
if d1[1] = '(' then // ou bien une seule parenthèse, ex : (2+3)
begin
courant.op := '(';
courant.FilsDroit := noeud.create;
d1 := copy(d1, 2, length(d1) - 2); // on supprime les parenthèses
Remplit(courant.FilsDroit, d1, '+', '-')
end
else // ou bien un seul nombre
traiter_sans_parentheses(courant, d1, '+', '-');
end;La fonction d'évaluation de l'arbre binaire devient donc :
function arbre.evalue(n: noeud): integer; //récursive, évidemment ;-)
begin
if n = nil then evalue := 0 else
if n.op = 'c' then // c'est une feuille "chiffre"
evalue := n.valeur
else begin // noeud opérateur
case n.op of
'(': evalue := evalue(n.FilsDroit);
'+': evalue := evalue(n.FilsGauche) + evalue(n.FilsDroit);
'-': evalue := evalue(n.FilsGauche) - evalue(n.FilsDroit);
'*': evalue := evalue(n.FilsGauche) * evalue(n.FilsDroit);
'/': evalue := evalue(n.FilsGauche) div evalue(n.FilsDroit);
end;
end;
end;Nous allons voir maintenant comment on construit un automate permettant de vérifier qu'une expression saisie au clavier est correcte d'un point de vue syntaxique.
VII-C-4. Automate de validation d'une expression arithmétique▲
Avant de soumettre une expression à notre calculette, nous devons en vérifier la validité (parenthèses correctement placées et pas d'erreurs syntaxiques).
Pour cela, nous allons utiliser un automate. En voici le schéma :
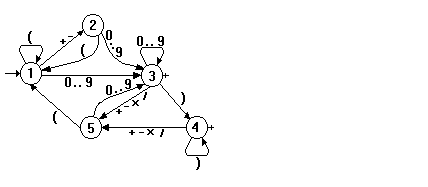
On va de l'état "1" à l'état "2" par un signe "+" ou "-".
Ce schéma comporte des cellules circulaires appelées états et des flèches appelées arcs ou transitions. Au dessus de chaque flèche se trouve une étiquette indiquant quels sont les caractères qui provoquent la transition.
L'état 1 est appelé "état initial" et il est identifiable par une flèche entrante.
Les états 3 et 4 sont appelés "états terminaux" et sont identifiables par une croix (ou un "+") placée à côté.
L'automate s'utilise en lui passant un par un, dans le sens de lecture naturel (de gauche à droite), les caractères qui constituent la chaîne à valider.
Certains états présentent des transitions sous forme de boucles, indiquant qu'on peut rester dans le même état en examinant deux caractères consécutifs : on va de l'état "1" à l'état "1" par "(" : cela indique qu'on peut avoir plusieurs parenthèses ouvrantes d'affilée : "((".
Appliquons cet automate pour voir si l'expression « 1+2 » est correcte.
Le premier caractère de l'expression est « 1 ». Nous soumettons ce caractère à l'automate qui se trouve alors dans l'état 1. Le chiffre "1" étant un entier entre 0 et 9, nous suivons la transition correspondante qui amène l'automate dans l'état 3.
Le caractère suivant est « + ». L'automate passe dans l'état 5.
Le dernier caractère est « 2 ». L'automate passe dans l'état 3.
C'est un état terminal, l'expression envisagée était donc correcte.
Si l'expression avait été « 1+ », nous serions resté dans l'état 5, qui n'est pas terminal, et l'expression aurait donc été jugée incorrecte.
Si l'expression avait été « 1+/ », nous n'aurions pu aller nulle part depuis l'état 5 (il n'y a aucune transition possible depuis l'état 5 avec le caractère « / ») et l'expression aurait également été jugée incorrecte.
Une expression est donc incorrecte dans deux cas :
elle laisse finalement l'automate dans un état non terminal
elle comporte un caractère qui, dans un état donné, ne provoque aucune transition.
Pour représenter l'automate, nous utilisons un tableau à deux dimensions :
const etats = 5; // nombre d'états de l'automate
caracs = 16; // 16 caractères autorisés pour la saisie
st = '0123456789+-*/()'; // les 16 caractères
tab: array[1..etats, 1..caracs] of integer =
//0 1 2 3 4 5 6 7 8 9 + - * / ( )
((3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 0, 0, 1, 0), {etat 1}
(3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 0, 0, 0, 0, 1, 0), {etat 2}
(3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 0, 4), {etat 3}
(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 5, 5, 5, 0, 4), {etat 4}
(3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 0, 0, 0, 0, 1, 0)); {etat 5}Chaque case du tableau indique quel état est amené par la transition provoquée par le caractère en cours en partant de l'état courant :
etat :=tableau[etat,caractere];
Si, par exemple, l'automate se trouve dans l'état 2 (ligne 2 du tableau) et qu'on lit une parenthèse ouvrante, alors l'automate passe dans l'état 1 (donc, pour le prochain caractère on lira dans la ligne 1 du tableau). Si l'automate se trouve dans l'état 1 et qu'on lit un « / », alors l'automate passe dans l'état 0 (il y a une erreur) et on s'arrête.
Les zéros indiquent qu'un caractère donné ne provoque aucune transition à partir d'un état donné (impasse).
Il ne nous reste plus qu'à soumettre à notre automate l'expression à valider, caractère par caractère.
Label1.Caption:=Automate(Edit1.Text);
Si, à un moment quelconque de l'analyse de notre expression mathématique, etat=0, alors nous sommes dans une impasse, et l'expression est donc incorrecte.
Si, à la fin, l'automate ne se trouve pas dans l'état 3 ou l'état 4 (les seuls états terminaux), l'expression est incorrecte.
Nous avons ajouté une variable « equilibre », chargée de mesurer la différence entre le nombre de parenthèses ouvrantes et le nombre de parenthèses fermantes.
En effet, on démontre mathématiquement qu'un automate du type de celui que nous utilisons n'est pas capable de reconnaître les fautes de parenthésage. Il faut utiliser un automate "à pile" (muni d'un compteur). La variable "equilibre" joue ce rôle de compteur.
Au début equilibre=0 (il y a équilibre, puisqu'il n'y a aucune parenthèse).
Pour chaque parenthèse ouvrante trouvée, nous ajoutons 1 à la variable "equilibre".
Pour chaque parenthèse fermante trouvée, nous retranchons 1 à la variable "equilibre".
- En cours de validation, "equilibre" est strictement négatif : cela signifie que nous avons rencontré plus de fermantes que d'ouvrantes. Inutile d'aller plus loin : l'expression est incorrecte.
- En fin de validation, "equilibre" est nul : tout s'est bien passé au niveau des parenthèses, il y a autant d'ouvrantes que de fermantes, et elles ne sont pas placées n'importe comment. En effet, comme "equilibre" est évalué dans l'ordre de lecture, une séquence comme "())(" aurait déjà été rejetée - à cause d'un équilibre négatif - au cours de la validation. Si donc "equilibre" est nul, et que l'expression est incorrecte, le problème ne vient pas d'une faute de parenthésage.
- En fin de validation, "equilibre" est strictement positif : cela signifie que nous avons rencontré plus d'ouvrantes que de fermantes : l'expression est incorrecte.
Voici la fonction "automate" programmée :
function Automate(s: string): string;
const etats = 5;
caracs = 16; // 16 caractères autorisés pour la saisie
st = '0123456789+-*/()'; // les 16 caractères
tab: array[1..etats, 1..caracs] of integer =
//0 1 2 3 4 5 6 7 8 9 + - * / ( )
((3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 0, 0, 1, 0), {etat 1}
(3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 0, 0, 0, 0, 1, 0), {etat 2}
(3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 0, 4), {etat 3}
(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 5, 5, 5, 0, 4), {etat 4}
(3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 0, 0, 0, 0, 1, 0)); {etat 5}
var p, n: integer; car: char; etat, equilibre: integer;
begin
if s = '' then
begin
result := 'Chaîne vide';
exit;
end;
equilibre := 0; //comptage des parenthèses
p := 0; //position courante dans la chaîne s
etat := 1;
repeat
inc(p);
car := s[p]; //caractère en cours
if car = '(' then inc(equilibre);
if car = ')' then dec(equilibre);
if equilibre >= 0 then
begin
n := pos(car, st);
// la position du caractère en cours dans la chaîne de caractères autorisés
if n > 0 then etat := tab[etat, n]; //c'est un caractère autorisé
end;
until (p = length(s)) or (equilibre < 0) or (n = 0) or (etat = 0);
if equilibre < 0 then
result := 'Il y a une parenthèse fermante en trop à la position ' + inttostr(p)
else
if (equilibre > 0) then
result := 'Il y a une parenthèse ouvrante en trop'
else
if n = 0 then
result := 'Caractère non autorisé à la position ' + inttostr(p)
else
if etat = 0 then
result := 'Expression incorrecte (erreur à la position ' + inttostr(p) + ')'
else
if (etat <> 3) and (etat <> 4) then
result := 'Expression incorrecte (etat final non terminal)'
else
result := 'Expression correcte';
end;VII-C-5. Source de l'exemple▲
Code des exemples : chap_VII_3.zip Miroir 1 , chap_VII_3.zip Miroir 2
VII-D. Les arbres n-aires : codage d'un dictionnaire▲
Nous allons étudier dans ce Chapitre la façon de coder un dictionnaire dans un arbre n-aire (chaque noeud de l'arbre possède n branches).
VII-D-1. Structure des données▲
Pour commencer, nous allons étudier la structure d'un noeud. On suppose que le dictionnaire est en majuscules, c'est pourquoi nous n'avons que 26 lettres possibles pour un noeud. Bien évidemment, cette structure peut être élargie si on veut aussi prendre en compte les minuscules et les chiffres ou autres signes. Nous voulons aussi afficher l'arbre n-aire à l'écran (sur un exemple comportant seulement quelques mots), ce qui implique que chaque noeud aura une position à l'écran, matérialisée par deux coordonnées x et y. Chaque noeud contient une lettre, donc une variable de type char, et il doit contenir aussi un indicateur boolean utilisé pour indiquer si un mot est entier : par exemple, supposons qu'on code le mot "CARTE" dans un arbre; l'arbre aura donc 5 niveaux. La dernière lettre du mot (le "E") aura son indicateur boolean positionné à true. Par contre, la lettre "A" n'aura pas son indicateur positionné, car le mot "CA" n'est pas un mot du dictionnaire. La lettre "R" aura son indicateur positionné, car le mot "CAR" fait partie du dictionnaire de la langue française.
Un noeud possède donc:
- 26 fils, les lettres possibles de 'A' à 'Z'
- les coordonnées (x,y) qui seront utilisées pour l'affichage graphique de l'arbre
- une lettre
- un indicateur boolean
Noeud =
class
private
Fils: array['A'..'Z'] of Noeud; //liste de fils
x, y: integer; // pour dessin arbre
Lettre: char; // lettre contenue dans ce noeud de l'arbre
Entier: boolean; //flag indiquant si le mot est entier
public
constructor create;
destructor destroy;
end; { Noeud }
Etudions maintenant la structure d'un arbre. Comme nous l'avons déjà vu, un arbre est constitué par sa tête, et par une autre variable nous permettant de parcourir l'arbre. Les opérations relatives à un arbre sont les suivantes :
- ajout d'un mot
- chargement d'un fichier dans l'arbre en utilisant l'opération d'ajout
- compter le nombre de noeuds terminaux se trouvant en-dessous d'un noeud quelconque
- l'affichage graphique et l'affichage texte (création d'une liste de mots du dictionnaire)
- recherche d'un mot
Dans notre exemple, nous avons choisi une liste de 13 mots de 5 lettres chacun. A l'aide de la fonction qui compte le nombre de noeuds terminaux, on peut donc dire combien de mots comporte l'arbre.
//arbre d'ordre 26
Arbre =
class
private
tete, courant: noeud;
public
constructor create;
destructor destroy; override;
procedure rajouter_mot(LeMot: string);
procedure charger(NomFic: string);
procedure Affiche(S, prefixe: string);
procedure dessine(en_cours: noeud; limg, old_x, old_y: integer);
function Trouve(LeMot: string): boolean;
function compter_terminaux(en_cours: noeud): integer;
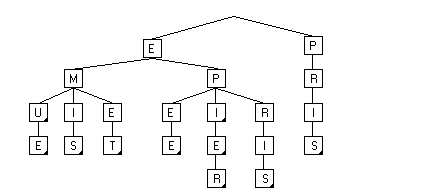
end;Nous allons voir, une par une, toutes les procédures décrites ci-dessus. Mais auparavant, voici un exemple concret d'arbre n-aire qui contient des mots de longueur 3 (EMU,EPI), de longueur 4 (EMUE, EMIS, EMET, EPIE, PRIS) et de longueur 5 (EPIER, EPRIS), dont l'indicateur est positionné à true, et qui est représenté sur ce schéma par un petit triangle noir dans le coin des cases en bas à droite.
VII-D-2. La procédure d'ajout d'un mot▲
On part du sommet de l'arbre. La procédure est récursive, et comme toute procédure récursive, elle a un point d'appui (ou d'arrêt). On va ajouter le mot dans l'arbre lettre par lettre, en descendant dans l'arbre d'un niveau à chaque lettre. Le mot est donc "mangé" progressivement du début vers la fin.
1) Le point d'arrêt est atteint quand on n'a plus de lettres à ajouter dans l'arbre. Dans ce cas, on positionne le noeud courant à true, pour indiquer que c'est un mot complet et on quitte la procédure.
2) On a encore des lettres à ajouter dans l'arbre. Prenons le cas du mot "EPI". On est au sommet de l'arbre. Si la lettre "E" existe déjà dans l'arbre en tant que noeud fils du sommet, alors :
- on "mange" le "E"; le mot à rajouter devient "PI" mais il faut le mettre sous le "E"
- on descend sur le fils "E"
- on rajoute (récursivement) le mot "PI"
Si la lettre "E" n'existe pas, alors :
- on crée le noeud fils "E"
- on exécute les étapes ci-dessus.
ci le programme correspondant :
procedure arbre.rajouter_mot(LeMot: string);
var lettre: char;
begin
if LeMot = '' then
begin
courant.entier := true;
exit;
end;
lettre := LeMot[1];
if courant.fils[lettre] <> nil then // si la lettre existe déjà
courant := courant.fils[lettre] // alors on se positionne sur la lettre suivante
else // sinon il faut créer cette lettre dans l'arbre
begin
courant.fils[lettre] := noeud.create;
courant := courant.fils[lettre];
courant.lettre := lettre; // la lettre est maintenant dans l'arbre
end;
delete(LeMot, 1, 1); // on efface la lettre du mot puisqu'elle est déjà dans l'arbre
rajouter_mot(LeMot); // et on rajoute le reste
end;VII-D-3. La procédure de chargement d'un fichier▲
Le fichier étant un simple fichier texte, il suffit de le lire ligne par ligne et d'ajouter au fur et à mesure les mots lus dans l'arbre.
procedure arbre.charger(NomFic: string);
var s: string;
chemin: string; // le chemin de l'appli, AVEC l'antislash final
f: textfile;
begin
chemin := ExtractFilePath(Application.ExeName);
assignFile(f, chemin + nomFic);
reset(f);
repeat
readln(f, s);
courant := tete; // on se positionne en tête de l'arbre
rajouter_mot(s); // et on rajoute le mot
until eof(f);
closeFile(f);
end;VII-D-4. Comptage des noeuds terminaux▲
Pour dessiner un arbre, nous avons besoin de cette fonction. En effet, si un père a deux noeuds terminaux, sa position à l'écran sera au milieu de ses deux fils (il s'agit de la position sur l'axe des abscisses, les "x"; en tant que père il sera positionné au dessus de ses fils sur l'axe des ordonnées, les "y"). Cela est valable aussi pour un père qui n'a pas directement de noeuds terminaux, mais dont les fils ou sous-fils en ont. Il faut donc parcourir récursivement le sous-arbre dont le père est le noeud courant pour arriver jusqu'aux noeuds terminaux.
Une solution serait la suivante :
- la somme des noeuds terminaux ayant pour ancêtre un noeud donné est :
--- égale à un si le noeud en question n'a pas de fils (point d'arrêt)
--- égale à la somme des noeuds terminaux de ses fils sinon
Mais, dans ce cas, on peut supprimer le point d'arrêt et faire fusionner les deux conditions. En effet, on n'a qu'à parcourir tous les fils du noeud en cours et, s'ils ne sont pas égaux à nil, incrémenter alors une variable locale avec leurs propres noeuds terminaux. Si, à la fin, le total obtenu est égal à zéro, alors aucun des fils du noeud en cours n'existe (point d'arrêt de la récursivité) donc on initialise la variable locale à 1 et on sort.
function arbre.compter_terminaux(en_cours: noeud): integer;
var i: char;
total: integer;
begin
total := 0;
for i := 'A' to 'Z' do
if en_cours.fils[i] <> nil then
inc(total, compter_terminaux(en_cours.fils[i]));
if total = 0 then inc(total);
compter_terminaux := total;
end;VII-D-5. Affichage graphique d'un arbre n-aire▲
La procédure d'affichage d'un arbre nécessite, pour commencer, une image et ensuite quelques petits calculs mathématiques, ainsi que le nombre total de noeuds terminaux qui se trouvent en-dessous du noeud courant. La première chose à faire est de compter le nombre de noeuds terminaux dérivant du noeud en cours, afin de décider où il sera placé graphiquement, ceci nous amenant donc au calcul de ses coordonnées. Ensuite pour chaque noeud dessiné, on doit tracer une ligne le reliant à son père, ce qui nous amène à l'utilisation de 2 paramètres (old_x,old_y) de type integer. On suppose que chaque noeud occupe 50 pixels en largeur et 80 en hauteur. Ainsi, si un noeud a 4 fils, sa position sera à la moitié de 4*50, soit " (4*50) div 2". S'il n'a que 2 fils, il sera à " (2*50) div 2". Mais comment faire pour que les noeuds d'un même niveau se décalent vers la droite ? En effet dans le dessin suivant, au niveau 1, nous avons deux fils, le premier ayant 2 fils terminaux et le deuxième trois fils terminaux.
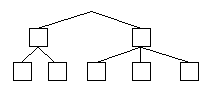
Si on applique la formule ci-dessus, alors le premier noeud du niveau 1 est situé à "x:=(2*50)/2" (soit x=50) et le deuxième est situé à "x:=(3*50)/2" (soit x=75). On constate alors que ces deux noeuds se chevauchent, puisque le premier est situé à x=50 et il occupe 50 pixels (jusqu'à cent; or le deuxième est situé à x=75). Donc, à chaque dessin d'une partie de l'arbre, il faut voir quelle est la largeur qu'il requiert et la passer en paramètre à ses frères, de façon à ce que ceux-ci commencent leur dessin avec un décalage vers la gauche. Ainsi dans l'exemple ci-dessus, le premier noeud nécessite 100 pixels (car il a deux fils terminaux, qui seront dessinés à partir de la position 0 ), et le deuxième noeud nécessite 150 pixels (car il a trois noeuds terminaux, qui seront dessinés à partir de la position 100). Ceci nous amène à un nouveau paramètre, appelé "limg" qui indique la position à partir de laquelle on doit dessiner le sous arbre du noeud en cours. On effectue ensuite les opérations suivantes :
- on calcule la position du noeud en cours (x et y)
- on relie ce noeud à son père
- on parcourt tous ses fils et pour chaque fils non vide on dessine le sous-arbre correspondant en faisant un appel récursif.
procedure arbre.dessine(en_cours: noeud; limg, old_x, old_y: integer);
var x, y, nb: integer;
i: char;
begin
//nb:=compter_terminaux(courant); // effet joli
nb := compter_terminaux(en_cours);
x := limg + (50 * nb) div 2;
y := old_y + 80;
if en_cours <> tete then
with form1.image1.picture.bitmap.canvas do
begin
textout(x, y, en_cours.lettre);
en_cours.x := x; en_cours.y := y;
moveto(x, y - 5); lineto(old_x, old_y);
end;
for i := 'A' to 'Z' do
if en_cours.fils[i] <> nil then
begin
nb := compter_terminaux(en_cours.fils[i]);
dessine(en_cours.fils[i], limg, x, y + 20);
limg := limg + nb * 50;
end;
end;VII-D-6. Affichage de texte (création d'une liste de mots du dictionnaire)▲
Pour réaliser un affichage de tous les mots de l'arbre, on n'a qu'à parcourir ses noeuds et quand on arrive à un noeud dont l'indicateur boolean est positionné, on ajoute le mot à une liste. Ensuite, on parcourt tous les fils du noeud en cours en faisant un appel récursif. Comme les mots se constituent au fur et à mesure qu'on descend dans l'arbre, on utilise un paramètre à cet effet.
procedure arbre.Affiche(S: string);
var i: char;
aux: noeud;
begin
if courant.Entier then Form1.Memo1.Lines.Add(s);
for i := 'A' to 'Z' do
if courant.fils[i] <> nil then
begin
aux := courant;
courant := courant.fils[i];
Affiche(S + i);
courant := aux;
end;
end;VII-D-7. Recherche d'un mot dans l'arbre▲
La recherche se fait par une descente récursive dans l'arbre; à chaque descente, on regarde si le noeud en cours a un fils qui est identique à la première lettre du mot. Si c'est le cas, alors on "mange" le début du mot (la première lettre) et on cherche à partir de la position courante le mot restant. Si, à un moment, pendant l'exploration de l'arbre, on se retrouve avec un mot vide, alors le mot appartient à l'arbre. Attention : cette condition n'est valable que pour les arbres dont tous les mots ont la même longueur. Sinon, il faut rajouter une condition supplémentaire, et cette tâche vous revient.
function arbre.trouve(LeMot: string): boolean;
var lettre: char;
begin
if LeMot = '' then
trouve := true
else
begin
lettre := LeMot[1];
delete(LeMot, 1, 1);
if courant.fils[lettre] = nil then
trouve := false
else
begin
courant := courant.fils[lettre];
trouve := trouve(LeMot);
end;
end;
end;VII-D-8. Source de l'exemple▲
Code des exemples : chap_VII_4.zip Miroir 1 , chap_VII_4.zip Miroir 2