Cours sur la récursivité

Nous allons voir, pour commencer, un exemple simple de dérécursification. Nous allons prendre pour exemple la suite de Fibonacci, dont voici la définition :
f ( 1 ) =1
f ( 2 ) =1
f ( n ) = f ( n-1 ) + f ( n-2 ), pour tout entier naturel n strictement supérieur à 2.

Sa traduction en langage informatique nous donne :

function fibo_rec(n: integer): integer;
begin
  if (n < 3) then fibo_rec := 1
  else
    fibo_rec := fibo_rec(n - 1) + fibo_rec(n - 2);
end;

Pour transformer cette procédure récursive en une procédure itérative, nous devons d'abord regarder quelles sont les valeurs successives de cette suite :
1,1,2,3,5,8,13,21,34,55,...

D'après la définition, on voit que chaque terme de la suite est une somme de deux nombres (f(n-1) et f(n-2)).

Nous devons donc avoir deux variables dans notre procédure itérative. Nous allons les appeler n1 et n2. Ces deux nombres verront leur valeur s'incrémenter progressivement.

Essais et observations

1. On veut calculer f(3). n1=1, n2=1, donc f:=n1+n2=2;
2. On veut calculer f(4); n1=1; n2=2; f (4)=1+2=3
3. On veut calculer f(5) : n1=2; n2=3; f(5)=2+3=5

Pour une valeur quelconque x, f(x)=n1+n2; il faut donc faire une boucle dans laquelle nous allons modifier progressivement les valeurs de n1 et n2.

Ainsi pour le cas 1) ci-dessus, on a algorithmiquement :

n1=1; n2=1; f:=n1+n2=2

Pour le cas 2) ci-dessus on a algorithmiquement:

n1=1; n2=1;  //--- valeurs de base
aux:=n2;  //--- sauvegarde de la valeur de n2
n2:=n1+n2=2;   //--- calcul de f(n-1)+f(n-2)
n1:=aux=1;  //--- nouvelle valeur de n1, correspondant à l'ancienne valeur de n2 avant la modif de la ligne du dessus

f:=n1+n2=3

Pour le cas 3) ci-dessus on a :

n1=1; n2=1;  //--- valeurs de base
aux:=n2;  //--- sauvegarde de la valeur de n2
n2:=n1+n2=2;   //--- calcul de f(3)=f(2)+f(1)
n1:=aux=1;  //--- nouvelle valeur de n1, correspondant à l'ancienne valeur de n2 avant la modif de la ligne du dessus
aux:=n2;  //--- sauvegarde de la valeur de n2
n2:=n1+n2=3;   //--- calcul de f(4)=f(3)+f(2)
n1:=aux=2;  //--- nouvelle valeur de n1, correspondant à l'ancienne valeur de n2 avant la modif de la ligne du dessus

f:=n1+n2=5

On remarque que le groupe de 3 lignes peut très bien constituer une boucle répétée deux fois. Donc on peut la généraliser x fois si nécessaire; dans ce cas nous obtenons le programme suivant :

function fibo_it(n: integer): integer;
var i, aux, n1, n2: integer;
begin
  n1 := 1; n2 := 1;
  for i := 3 to 10 do
  begin
    aux := n1 + n2;
    n1 := n2;
    n2 := aux;
  end;
  fibo_it := aux;
end;

Comme on peut le constater, la dérécursification est parfois très simple, elle revient à écrire une boucle, à condition d'avoir bien fait attention à l'évolution des variables au cours de l'exécution. Mais parfois elle est extrêmement difficile à mettre en oeuvre, comme c'est le cas pour certaines fractales ou les tours de Hanoï.

Code des exemples : chap_VIII_1.zip Miroir 1 , chap_VIII_1.zip Miroir 2

Nous savons que la structure d'un arbre binaire est récursive. Nous allons voir comment on peut implémenter cette structure récursive dans une structure statique (c'est à dire un tableau de taille fixe). Voici d'abord la structure dynamique de l'arbre binaire (telle que nous l'avons vue dans le chapitre précédent) :

type Noeud =
  class
  private
    Fils: array['A'..'Z'] of Noeud; //liste de fils
    x, y: integer; // pour dessin arbre
    Gauche, Droite: Noeud;
    Lettre: char; // lettre contenue dans ce noeud de l'arbre
    Entier: boolean; //flag indiquant si le mot est entier
  public
    constructor create;
    destructor destroy;
  end; { Noeud }

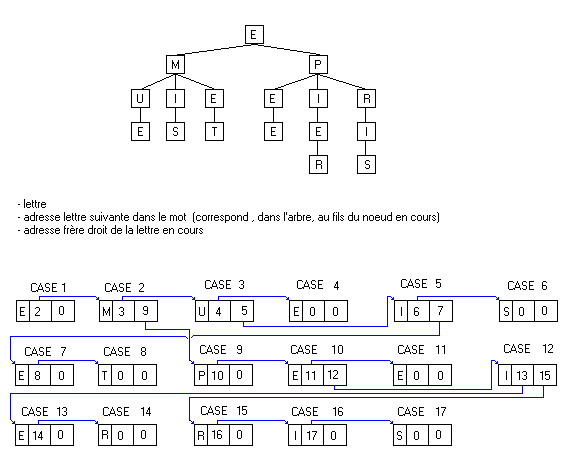
Nous allons maintenant transformer cette structure dynamique en une structure statique, donc linéaire. Pour cela nous allons utiliser un tableau, dont chaque case a une structure représentée par :
- "lettre" : une variable de type "char"
- "fin" : une variable de type booléen, mais représentée ici par un byte, qui indique que le mot est entier
- "droite","bas" : représentent les deux fils gauche et droit de la structure dynamique.

type trec = record
    lettre: char;
    fin: byte;
    droite, bas: longint;
  end;
 
  dictionnaire = record
    t: array[1..5000] of trec;
    derniere_case: longint;
  end;
 
var dico: dictionnaire;

Nous avons utilisé un tableau de 5.000 cases; mais en plus le dictionnaire contient aussi une variable "derniere_case", de façon à ce qu'on sache où on doit implémenter dans le tableau tous les nouveaux mots.

Nous allons utiliser dans le programme à télécharger des mots de la même longueur, mais néanmoins, pour expliquer le principe de l'implémentation dans un tableau, nous utiliserons des mots de longueur différente. Voici une image illustrant parfaitement les types prédéfinis ci-dessus, ainsi que l'implémentation d'un petit arbre n-aire :

Nous allons décrire brièvement une recherche de mot dans ce tableau. Supposons qu'on veuille trouver le mot "EPRIS". Nus sommes au début sur la case 1, donc sur la lettre E. On cherche ses fils. Le premier est à la case 2 et c'est M. Mais nous, on cherche la lettre P, donc on va se positionner sur le frère de M (M,3,9) qui est à la case 9. C'est bien un P, donc on descend maintenant sur son premier fils qui se trouve à la case 10 (car P,10,0). On trouve un E, qui ne nous intéresse pas, donc on va sur le frère de E qui se trouve à la case 12 (car E,11,12). C'est un I, il ne nous intéresse donc pas et on se positionne sur son frère qui se trouve à la case 15 (car I,13,15) et c'est bien un R. Le fils de R se trouve à la case 16 (car R,16,0) et c'est un I; le fils de I est à la case 17 et c'est un S. On a donc bien le mot EPRIS, car derrière le S il n'y a plus de fils, sinon le mot aurait été incomplet. On utilise aussi la variable "fin" pour indiquer que le mot est complet, auquel cas on peut ajouter d'autres lettres derrière ce mot (exemple : EPI et EPIER; les cases I et R ont la variable "fin" positionnée à 1, les autres à 0).

1. procédure introduis_mot_fin_dico(mot : string;p : longint;bas : boolean);
2. function positionnement_sur_lettre(lettre : char;courant : longint; var dernier : longint ) : longint;
3. procédure rajoute_mot(mot : string);
4. function appartient(mot : string) : boolean;

• le mot à introduire dans le tableau
• la position à partir de laquelle on introduit le mot dans les cases du tableau
• une variable booléenne indiquant si le mot sera introduit en tant que fils de la case en cours (c'est donc la case "droite" qui est initialisée, cela correspondant à la lettre suivante dans le mot) ou bien en tant que frère (c'est donc la case "bas" qui sera initialisée);

exemple 1 : si on est sur la lettre I de EPIER et si on veut introduire la mot EPRIS, alors la lettre R sera introduite à droite de I en tant que fils de E. Si par la suite on cherche le mot EPRIS, on tombe premièrement sur le I, et comme il ne nous intéresse pas on prend le fils suivant de son père, donc R, suivi de I et de S.

exemple 2 : si on a introduit le mot EMIS, et si on est sur la lettre E et si on veut introduire le mot ROND, alors la lettre R sera mise en "bas" du E, en tant que frère de E.

Il faut savoir que dans tous les cas où l'on introduit un mot ou la fin d'un mot (pour le mot EPRIS on n'a introduit que RIS, car EP avait été introduit avec le mot EPEE), cette insertion se fera automatiquement à la fin du tableau (c'est à dire là où il y a des cases non remplies), donc à partir de la case numéro "derniere_case".

procedure introduis_mot_fin_dico(mot: string; p: longint; bas: boolean);
var l, courant: longint;
begin
  if bas
    then dico.t[p].bas := dico.derniere_case
  else dico.t[p].droite := dico.derniere_case;
  l := length(mot);
  for courant := 1 to l do
    with dico.t[dico.derniere_case + courant - 1] do
    begin
      lettre := mot[courant];
      fin := 0;
      droite := dico.derniere_case + courant;
      bas := 0;
    end;
  dico.t[dico.derniere_case + l - 1].droite := 0; // plus rien derrière
  dico.t[dico.derniere_case + l - 1].fin := 1; // c'est un mot
  inc(dico.derniere_case, l);
end;

La fonction 2) sert de positionnement sur une lettre, c'est à dire à trouver la case à partir de laquelle un mot sera introduit dans le tableau. Cette fonction a 3 paramètres :
- la lettre sur laquelle on veut se positionner
- la position à partir de laquelle on commence la recherche dans les cases
- la position de la dernière lettre trouvée (on a EPEE et on veut rajouter EPRIS; la dernière lettre trouvée est P et sa position dans le tableau sera retournée, car on va rajouter un R en tant que fils de P)

function positionnement_sur_lettre(lettre: char; courant: longint;
  var dernier: longint): longint;
var l: char;
begin
  l := dico.t[courant].lettre;
  if (courant > 0) and (l = lettre) then dernier := courant;
  while (courant <> 0) and (l <> lettre) do
  begin
    courant := dico.t[courant].bas;
    l := dico.t[courant].lettre;
    if (courant > 0)
      and (l = lettre)
      then dernier := courant; // mémorise la dernière position trouvée où l=lettre}
  end;
  positionnement_sur_lettre := courant;
end;

La procédure 3) représente le rajout d'un mot dans le tableau. Cette procédure utilise la procédure 1) et la fonction 2). Lors d'un rajout de mot dans notre tableau, nous devons réaliser dans l'ordre les opérations suivantes:

a) - nous positionner sur le noeud dont la lettre est identique à la première lettre du mot. Si le fils existe, alors on doit récupérer son numéro de case dans le tableau et recommencer avec la lettre suivante, sinon on doit récupérer le numéro de la case qui sera pointée par la case en cours.

exemple : dans le tableau décrit au dessin précédent, on a rempli les huit premières cases avec les mots EMUE,EMIS,EMET. La variable "derniere_case" est donc égale à 9. Si on veut rajouter EPEE, on doit récupérer le numéro 2, car P est le frère de M, et ainsi le numéro 9 se retrouve dans la case 2 : M,3,9. La case 9 est pointée par la case 2.

b) - arrivés ici, nous avons un choix à faire: ou bien nous avons trouvé au moins un début de mot qui était déjà dans le tableau (comme EP pour EPEE et EPRIS) et dans ce cas la variable "courant" est positive, ou bien on doit rajouter le mot en entier auquel cas la variable "courant" est nulle.

Si on a trouvé un début de mot, alors on est sur une case quelconque du tableau et on la fait pointer sur la case de numéro "derniere_case" où l'on rajoutera la suite du mot (exemple : on a dans le tableau le mot EPEE et on veut rajouter EPRIS. Le P pointe sur E et E n'a pas de frère, donc sa variable "bas" va pointer sur "derniere_case" où on va introduire le reste du mot, à savoir RIS).

Voici l'algorithme correspondant :

procedure rajoute_mot(mot: string);
var i, l, courant, p, precedent, dernier: longint;
  dedans: boolean;
begin
  l := length(mot); courant := 1; i := 1; dernier := 0;
  p := positionnement_sur_lettre(mot[1], 1, dernier);
  dedans := true;
  while (i <= l) and (p > 0) and
    (dedans) and
    (courant > 0) and
    (i < dico.derniere_case) do
  begin
    p := positionnement_sur_lettre(mot[i], courant, dernier);
    if p > 0 then courant := dico.t[p].droite;
    dedans := (dernier + 1) < dico.derniere_case;
    inc(i);
  end;
  if courant > 0 then //donc p=0
  begin
    dec(i);
    if dernier = 0 then // cas spécial
    begin
      if dico.derniere_case = 1
        then introduis_mot_fin_dico(mot, 1, false)
      else
      begin // positionnement sur la dernière lettre de la colonne d'un arbre
        p := courant;
        while p <> 0 do
        begin
          p := dico.t[p].bas;
          if p > 0 then courant := p;
        end;
        introduis_mot_fin_dico(mot, courant, true)
      end;
    end
    else
      if dernier + 1 = dico.derniere_case then
        if mot[i] = dico.t[dernier].lettre then
          introduis_mot_fin_dico(copy(mot, i, l), dernier, false)
        else
          introduis_mot_fin_dico(copy(mot, i, l), dernier, true)
      else
      begin // positionnement sur la dernière lettre de la colonne d'un arbre
        p := courant;
        while p <> 0 do
        begin
          p := dico.t[p].bas;
          if p > 0 then courant := p;
        end;
        introduis_mot_fin_dico(copy(mot, i, l), courant, true);
      end;
  end
  else // donc p<>0
    introduis_mot_fin_dico(copy(mot, i, l), dernier, false)
end;

Et maintenant il ne nous reste plus qu'à faire une fonction d'appartenance d'un mot. Elle est simple à réaliser; en effet, pour chacune des lettres du mot, à partir de la première et jusqu'à la dernière on appelle la fonction de positionnement sur une lettre donnée; si cette fonction échoue à un instant t, alors c'est que l'une des lettres du mot n'est pas dans les fils ou frères de la dernière lettre rencontrée; si, par contre, on arrive à la fin du mot, alors on doit tester que ce mot est bien terminé (la variable "fin" positionné à 1).

function appartient(mot: string): boolean;
var i, l, courant, p: longint;
  dernier: longint;
begin
  courant := 1; i := 1; p := 1; l := length(mot);
  while (i <= l) and (p > 0) do
  begin
    p := positionnement_sur_lettre(mot[i], courant, dernier);
    if p > 0 then courant := dico.t[p].droite;
    inc(i);
  end;
  appartient := (i > l) and (p > 0) and (dico.t[p].fin = 1);
end;

Code des exemples : chap_VIII_2.zip Miroir 1 , chap_VIII_2.zip Miroir 2

On veut réaliser de façon itérative le programme qui affiche le triangle de Pascal. On suppose pour cela que nous pouvons afficher seulement 25 lignes, donc on utilise un tableau de 26 entiers. Bien évidemment, on peut modifier sa taille si on veut. Pour afficher les lignes du triangle de Pascal, on entre manuellement le nombre de lignes, et on fait ensuite une boucle:
- qui appelle la procédure de calcul des lignes
- qui les affiche.

On sait que, pour les deux premières lignes, le tableau ne contient que des 1, donc on va l'initialiser manuellement. La procédure de calcul se charge du reste. Le programme sera donc :

tab_coef[1]:=1;tab_coef[2]:=1;
for ligne:=2 to nombre_lignes do
    calculer(ligne);

On sait que, dans le triangle de Pascal, chaque coefficient est égal à la somme du nombre immédiatement supérieur et du nombre au dessus à gauche.

0 : 1          (a+b)0 = 1 
1 : 1 1        (a+b)1 = 1*a + 1*b
2 : 1 2 1      (a+b)2 = 1*a2 + 2*a*b + 1*b2
3 : 1 3 3 1    (a+b)3 = 1*a3 + 3*a²*b + 3*a*b² + 1*b3
4 : 1 4 6 4 1  (a+b)4 = 1*a4 + 4*a3*b + 6*a²*b² + 4*a*b3 + 1*b4

Nous n'avons ici qu'un tableau à une dimension que nous allons progressivement modifier. On dispose dès le départ de la ligne 1, et si on veut calculer la ligne 2 on n'a qu'à rajouter un 1 à la fin du tableau (qui correspond à la diagonale) et modifier le contenu du tableau en faisant les sommes qui conviennent.

Il faut faire attention : supposons qu'on a déjà calculé la ligne 2, et qu'on veut calculer la ligne 3. Le deuxième élément de la ligne 3 est égal à la somme du premier élément de la ligne 2 et du deuxième élément de la ligne 2. On le calcule et on le met dans le tableau, pour obtenir : 1 3 1 1. Et quand on calcule le troisième élément, on obtient 1 3 4 1 au lieu de 1 3 3 1.

L'erreur vient du fait qu'on n'a pas utilisé l'ancienne valeur "2" du tableau, mais la nouvelle valeur "3" et "3+1=4". Il faut donc parcourir le tableau en sens inverse. En effet :
- on a 1 2 1.
- on rajoute un 1 à la fin : 1 2 1 1
- on parcourt le tableau en sens inverse à partir de l'avant dernière position (la troisième position) :

tab_coef[3]:=tab_coef[2]+tab_coef[3] = 3 donc on a 1 2 3 1

- on avance vers le début (en deuxième position):

tab_coef[2]:=tab_coef[1]+tab_coef[2] = 3 donc on a 1 3 3 1

On remarque que la valeur est la bonne. Nous nous sommes arrêtés à la valeur 2, donc la boucle sera de la forme :

for i:=j downto 2 do

Voici donc le programme affichant le triangle de Pascal de façon itérative :

procedure TForm1.Button1Click(Sender: TObject);
var ligne: integer;
  tab_coef: array[1..26] of integer;
 
  procedure calculer(j: integer);
  var i: integer;
    s: string;
  begin
    tab_coef[j + 1] := 1;
    for i := j downto 2 do
      tab_coef[i] := tab_coef[i - 1] + tab_coef[i];
    s := '';
    for i := 1 to j + 1 do s := s + inttostr(tab_coef[i]) + '  ';
    memo1.lines.add(s);
  end;
begin
  if strtoint(edit1.text) > 25 then
  begin
    showMessage('La valeur doit être inférieure à 25 !');
    exit;
  end;
  fillchar(tab_coef, sizeof(tab_coef), #0);
  tab_coef[1] := 1; tab_coef[2] := 1;
  for ligne := 2 to strtoint(edit1.text) do
    calculer(ligne);
end;

Code des exemples : chap_VIII_3.zip Miroir 1 , chap_VIII_3.zip Miroir 2

Nous allons réaliser un programme itératif pour "dérécursifier" le problème des tours de Hanoï. La difficulté vient du fait que le programme des tours de Hanoï contient un double appel récursif avec des paramètres différents : après avoir effectué le premier appel récursif, tout change (le nombre de disques, les piquets).

Nous avons vu dans les chapitres précédents que, pour aboutir à une procédure récursive, on exécutait à la main un ensemble d'instructions, on regardait quelles étaient celles qui se répétaient, quelles étaient les variables utilisées, et on regroupait finalement les blocs identiques pour aboutir à une procédure récursive. Pour dérécursifier les tours de Hanoï, on va faire la même chose : on va réaliser à la main les mouvements des disques sur les 3 piquets, et on va essayer de trouver des similitudes ou des répétitions, afin d'en tirer un algorithme itératif.

Rappelons d'abord la définition récursive de la procédure :

H (n,depart,arrivee)
   H (n-1,depart,intermédiaire)
   Deplacer(depart,arrivee)
   H (n-1,intermédiaire,arrivée)

VIII-D-1. Préliminaire▲

Nous allons noter Hn le déplacement de n disques (Hn est en fait le programme récursif, qui se résume à l'appel de la procédure). On symbolise "départ" par "d", "arrivée" par "a" et "intermédiaire" par "i".

La définition s'écrit alors :

 

Sélectionnez

Hn (d,a)
   Hn-1 (d,i)
   Deplacer(d,a)
   Hn-1 (i,a)

Voici un dessin avec les trois piquets.

On décide que, si on a un nombre pair de disques à déplacer, on les déplace de 1 vers 3, et que, si on a un nombre impair de disques à déplacer, on les déplace de 1 vers 2. Cela est cohérent avec la définition récursive car, par exemple, pour déplacer cinq disques de 1 vers 3, en appliquant la définition, on déplace quatre disques (nombre pair) de 1 vers 2, puis un disque (nombre impair) de 1 vers 3 et enfin le reste de 2 vers 3.

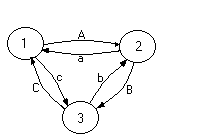
On note :
A le mouvement de 1 vers 2.
a le mouvement de 2 vers 1.
B le mouvement de 2 vers 3.
b le mouvement de 3 vers 2.
C le mouvement de 3 vers 1.
c le mouvement de 1 vers 3.

On décide de dire que :
les mouvements A et a sont de type 0.
les mouvements C et c sont de type 1.
les mouvements B et b sont de type 2.

Etudions quelques mouvements des disques :
H1 = A (de 1 vers 2)
H2 = A c B (1 vers 2; 1 vers 3; 2 vers 3)
H3 = A c B A C b A
H4 = A c B A C b A c B a C B A c B

On remarque que Hn, pour n supérieur à 2, est constitué d'une suite répétée de trois mouvements de types 0, 1 et 2. En effet, si l'on écrit Hn en majuscules, on obtient ACB ACB ACB..., avec éventuellement un A à la fin, la suite des mouvements ne pouvant se terminer que par A ou B (d'après ce que nous avons dit plus haut concernant la convention que nous avons adoptée suivant la parité de n).

Notons Gn la suite des mouvements de Hn, en faisant abstraction du sens du déplacement (ce qui revient à noter tous les mouvements en majuscules) :
Gn = A C B A C B A C B... (le dernier caractère étant un A pour n impair et un B pour n pair) pour n supérieur à 2, et G1=A. Gn n'est autre que Hn auquel il manque l'information de sens (distingué par les majuscules et les minuscules).

Ecrivons quelques valeurs de Gn :
G1 = A
G2 = A C B
G3 = A C B A C B A
G4 = A C B A C B A C B A C B A C B

VIII-D-2. Détermination du type du k-ième mouvement▲

VIII-D-3. Détermination du sens du déplacement : "A" ou "a" ?▲

VIII-D-4. Résumé▲

VIII-D-5. Conclusion▲

VIII-D-6. Source de l'exemple▲

Après avoir créé un programme récursif de traduction en français d'un nombre exprimé sous sa forme numérique, nous allons maintenant voir une façon itérative de réaliser cela, mais en changeant un peu les structures de données de façon à montrer qu'il existe d'autres possibilités de faire la même chose (ceci dans un but éducatif, bien évidemment)

Spécificité de l'algorithme

Nous allons construire la chaîne en prenant chaque chiffre à partir de la droite et en répétant la boucle jusqu'à ce que l'on arrive au premier chiffre de gauche. Cette démarche a pour avantage de générer à chaque fois un résultat temporaire que l'on peut assez facilement utiliser à la boucle suivante pour traiter en particulier les cas spéciaux liés aux accords du pluriel ('s') , aux traits d'union et autres ('un' , 'et' … ) . On n'aura plus qu'à faire la concaténation progressive des résultats obtenus. Par contre, cette évaluation s'effectue dans le sens inverse de la lecture naturelle des nombres (c'est à dire de la droite vers la gauche), c'est pourquoi à chaque groupe de trois chiffres on rajoutera l'unité correspondante : mille, million, milliard…

Algorithme

Pour commencer, on va créer des tableaux avec des chaînes de caractères.

On crée un tableau des unités avec les nombres qui ne peuvent pas se décomposer : zéro, un, deux, …, seize : on voit qu'il regroupe les unités et les nombres de dix à seize. Les nombres dix-sept, dix-huit, dix-neuf seront quant à eux logiquement traités en deux étapes (« dix » puis le chiffre restant).

On crée ensuite un tableau des dizaines qui contient les nombres vingt, trente, quarante, cinquante, soixante, quatre-vingt. ("soixante-dix" et "quatre-vingt-dix" n'y figurent pas, étant des cas spéciaux).

On crée ensuite un tableau qui contient les unités restantes : cent, mille, million, milliard, etc.

On suppose que le nombre est entier.

Si le nombre extrait est 0 alors on renvoie « zéro ».
275<>0 , donc on continue

Début de la boucle :

Considérons les deux exemples suivants : les nombres 275 et 398.

On va les découper en tranches de 3 chiffres, à partir de la fin et répéter ce qui suit jusqu'à ce qu'on soit tout à gauche du nombre initial (donc à son début) : à chaque étape de la boucle on divise le nombre par 1000, donc on va arriver à 0 tôt ou tard, auquel cas on s'arrête.

NB : par souci de clarté, on n'entrera pas ici dans le détail des accords du pluriel, des traits d'union etc…

1ère étape : On récupère d'abord le chiffre des unités, suivi immédiatement de celui des dizaines afin de traiter les cas spéciaux de la langue française.

nombre = 275,
unités = 5 , nombre restant = 27
dizaines = 7, nombre restant = 2
nombre = 398,
unités = 8, nombre restant = 39
dizaines = 9, nombre restant = 3

Soit temp une variable auxiliaire de type chaîne, qui est vide.

Temp := '' ;
Temp := '' ;

Si le chiffre des dizaines est « 1,7,9 » alors on décrémente ce chiffre et on incrémente de 10 le chiffre des unités.

Dizaines=6, unités=15
dizaines=8, unités=18

Si le chiffre des dizaines est supérieur à 1, alors on initialise temp avec la valeur correspondante (lue dans le tableau des dizaines)

Temp :='soixante' ;
temp :='quatre vingt' ;

Si on a un nombre des dizaines plus petit que 8 et si on a un « un » ou « onze » alors rajouter le mot « et »

On n'est pas concerné par ce cas.
On n'est pas concerné par ce cas.

Si le nombre des unités est supérieur à seize, alors on rajoute un espace et « dix » à temp et on décrémente le nombre des unités de 10. On se retrouve donc avec un nombre des dizaines décrémenté de 1, et le nombre des unités compris entre 1 et 16.

On n'est pas concerné par ce cas.

temp :='quatre vingt dix' ;
unités := unités-10 = 18-10 = 8 ;

Si le nombre des unités est plus grand que zéro alors on rajoute à temp la chaîne correspondante aux unités.

Temp :='soixante' + 'quinze' = 'soixante quinze' ;
temp :='quatre vingt dix' + 'huit' = 'quatre vingt dix huit' ;

On mémorise le résultat dans une autre variable.

Result := 'soixante quinze' ;
Result :='quatre vingt dix huit' ;

2ème étape : on étudie maintenant le 3è chiffre à partir de la droite …
On récupère le chiffre des centaines et on divise le nombre restant par 10.

C :=2 ; nombre restant := 0 ;
C :=3 ; nombre restant := 0 ;

Si le chiffre des centaines est supérieur à 1, alors on va récupérer l'unité correspondante :

Temp :='deux' ;
Temp :='trois' ;

On rajoute 'cent' à cette variable :

Temp :='deux cent' ;
Temp :='trois cent' ;

Si le résultat mémorisé est nul, alors on rajoute un 's' sinon on ne fait rien

On n'est pas concerné par ce cas.
On n'est pas concerné par ce cas.

On colle ces deux résultats :

Result :='deux cent'+'soixante quinze' = 'deux cent soixante quinze';
Result :='trois cent'+'quatre vingt dix huit' = 'trois cent quatre vingt dix huit';

On regarde si on doit rajouter mille, million ou milliard. Ceci se fait à l'aide d'un compteur auxiliaire qui est incrémenté à chaque pas de la boucle.

On n'est pas concerné par ce cas.
On n'est pas concerné par ce cas.

Fin de la boucle

Code des exemples : chap_VIII_5.zip Miroir 1 , chap_VIII_5.zip Miroir 2